Задача 70176 ...
Условие
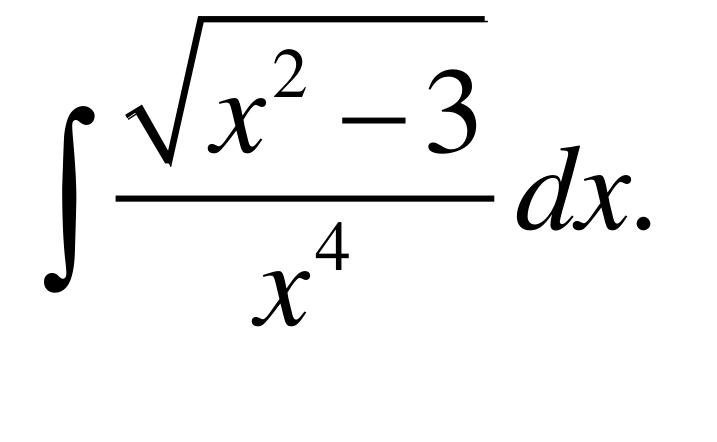
Решение
[m]x=\frac{\sqrt{3}}{sint}[/m]
[m]dx=(\frac{\sqrt{3}}{sint})`dt[/m] ⇒ [m]dx=\frac{\sqrt{3}}{sin^2t}\cdot cost dt[/m]
[m]\sqrt{x^2-3}=\sqrt{(\frac{\sqrt{3}}{sint})^2-3}=\sqrt{\frac{3-3sin^2t}{sin^2t}}=\sqrt{3}\frac{cost}{sint}[/m]
Тогда интеграл принимает вид:
[m]= ∫ \frac{\sqrt{3}\frac{cost}{sint}}{(\frac{\sqrt{3}}{sint})^4}\frac{\sqrt{3}}{sin^2t}\cdot cost dt= ∫cos^2t\cdot sint dt= ∫ cos^t (-d(cost))= [/m][red][m]-\frac{cos^3t}{3}+C[/m] [/red]
Обратный переход к переменной х:
[m]x=\frac{\sqrt{3}}{sint}[/m] ⇒ [m]sint=\frac{\sqrt{3}}{x}[/m] ⇒
так как [m]cost=\sqrt{1-sin^2t}[/m]
[m]cost=\sqrt{1-(\frac{\sqrt{3}}{x})^2}[/m]
[m]cost=\frac{\sqrt{x^2-3}}{x}[/m]
О т в е т. [red][m] -\frac{(\frac{\sqrt{x^2-3}}{x})^3}{3}+C[/m] [/red]
