Задача 34812 ...
Условие
∫ dx / ((2x + 1)^2 - √(2x + 1))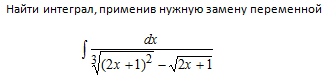
математика ВУЗ
788
Решение
★
(2x+1)=t^6
Тогда
[b]∛(2x+1)^2=t^4[/b]
[b]sqrt(2x+1)=t^3[/b]
x=(t^6-1)/2
dx=6t^5dt/2
[b]dx=3t^5dt[/b]
получаем
∫ 3t^5dt/(t^4-t^3)= 3* ∫ t^2dt/(t-1)= 3* ∫ (t^2-1+1)dt/(t-1)=
=3* ∫ (t^2-1)dt/(t-1) + 3*∫(dt/(t-1))=
=3* ∫ (t+1)dt +3 ∫ dt/(t-1)=
=3(t^2/2)+3t + 3ln|t-1| + C
Обратный переход
= [b](3/2)∛(2x+1)+3(2x+1)^(1/6) - 3*ln|(2x+1)^(1/6) - 1| + C[/b]
