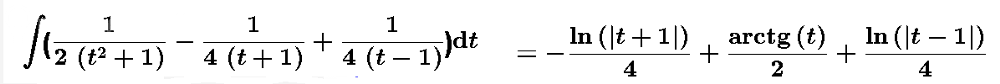Задача 71121 ...
Условие
неопределенный интеграл
(√х) / (x-3√x) dx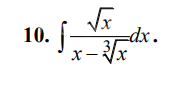
математика ВУЗ
288
Решение
★
[m]x=t^6[/m]
[m]dx=6t^5dt[/m]
[m]\sqrt{x}=t^3[/m]
[m]\sqrt[3]{x}=t^2[/m]
[m] ∫ \frac{\sqrt{x}}{x-\sqrt[3]{x}}dx= ∫ \frac{t^3}{t^6-t^2} 6t^5dt=6 ∫\frac{t^6}{t^4-1}dt[/m]
Под знаком интеграла неправильная дробь.
Выделяем целую часть
[m]6 ∫ (t^2+\frac{t^2}{t^4-1})dt=[/m]
Раскладываем дробь на простейшие
[m]t^4-1=(t^2+1)(t-1)(t+1)[/m]
[m]\frac{t^2}{t^4-1}=\frac{Mt+N}{t^2+1}+\frac{A}{t-1}+\frac{B}{t+1}[/m]
M=0
N=1/2
B=-1/4
A=1/4
О т в е т. 6*(t^3/3)-(6/4)ln|t+1}+3arctg t+(6/4)ln|t-1|+C
[m]t=\sqrt[6]{x}[/m]