Задача 38033 Вычислить интеграл от иррациональной...
Условие
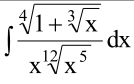
математика ВУЗ
1115
Решение
★
См. приложение подстановки ( Чебышева)
x*x^(5/12)=x^(17/12)
m=-17/12; n=1/3; p=1/4
пункт 3
(m+1)/n+p=(-5/12)/(1/3) + (1/3)=(-5/4)+(1/4)=-4/4=-1 - целое
1+x^(1/3)=t^4x^(1/3) ⇒ x^(-1/3)+1=t^4 ⇒ t=(x^(-1/3)+1)^(1/4)
x^(1/3)=1/(t^4-1)
x^(1/3)=(t^4-1)^(-1)
x=(t^4-1)^(-3)
dx=-3(t^4-1)^(-4)*(t^4-1)`dt
dx=-12t^3(t^4-1)^(-4)dt
(1+x^(1/3))^(1/4)= (t^(4)x^(1/3))^(1/4)=tx^(1/(12))
x^(-17/12))*(1+x^(1/3))^(1/4)=x^(-17/12)*tx^(1/12)=tx^(-4/3)=t(t^4-1)^(4)
Тогда интеграл примет вид
-12 ∫t^4dt=12*(t^5/5) + C
где t=(x^(-1/3)+1)^(1/4)
