Задача 45244 Найти интегралы...
Условие
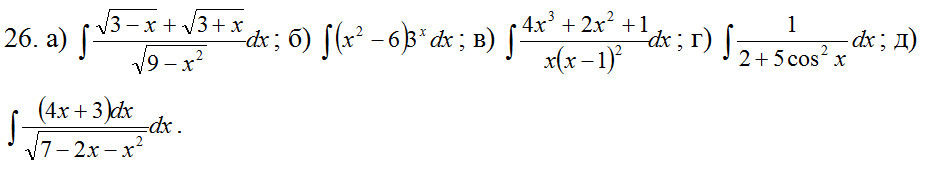
Решение
[m]\int \frac{\sqrt{3-x}+\sqrt{3+x}}{\sqrt{9-x^2}}dx=\int \frac{\sqrt{3-x}}{\sqrt{9-x^2}}dx+\int \frac{\sqrt{3+x}}{\sqrt{9-x^2}}dx=[/m]
[m]\int \frac{1}{\sqrt{3+x}}dx+\int \frac{1}{\sqrt{3-x}}dx=\int \frac{d(3+x)}{\sqrt{3+x}}dx-\int \frac{d(3-x)}{\sqrt{3-x}}dx=[/m]
[m]=2\sqrt{3+x}-2\sqrt{3-x}+C[/m]
б).
по частям
[m]u=x^2-6[/m]
[m]dv=3^{x}dx[/m] ⇒
[m]du=2xdx[/m]
[m]v=\frac{3^{x}}{ln3}[/m]
[m]∫ (x^2-6)3^{x}dx=[/m]
[m]=(x^2-6)\cdot \frac{3^{x}}{ln3}-\int \frac{2x\cdot 3^{x}}{ln3}dx=[/m]
[m]=(x^2-6)\cdot \frac{3^{x}}{ln3}-\frac{2}{ln3}\int 3^{x}dx=[/m]
второй интеграл так же считаем по частям:
по частям
[m]u=x[/m]
[m]dv=3^{x}dx[/m] ⇒
[m]du=dx[/m]
[m]v=\frac{3^{x}}{ln3}[/m]
=[m](x^2-6)\cdot \frac{3^{x}}{ln3}-\frac{2}{ln3}( x\cdot \frac{3^{x}}{ln3}-\int\frac{3^{x}}{ln3}dx)=[/m]
=[m](x^2-6)\cdot \frac{3^{x}}{ln3}-\frac{2 \cdot 3^{x}}{ln^23} \cdot x +\frac{2}{ln^23}\int 3^{x}dx=[/m]
[m](x^2-6)\cdot \frac{3^{x}}{ln3}-\frac{2\cdot 3^{x}}{ln^2 3}\cdot x +\frac{2\cdot 3^{x}}{ln^33}+C[/m]
в) под интегралом неправильная дpобь, степень числителя равна степени знаменателя:
надо выделить целую часть.
Разделив числитель на знаменатель.
Затем правильную дробь разложить на простейшие:
г)
Так как
1+tg^2x=[m]\frac{1}{cos^2x}[/m], то
cos^2x=[m]\frac{1}{1+tg^2x}[/m]
Замена переменной
tgx=t
x=arctgt
dx=dt/(1+t^2)
д) в знаменателе в подкоренном выражении
7-2x-x^2
выделяем полный квадрат:
7-2x-x^2=-(x^2+2x-7)=-(x^2+2x+1-8)=8-(x-1)^2
Замена переменной:
x-1=t
x=t+1
dx=dt
[m]=\int \frac{4(t+1)+3}{\sqrt{8-t^2}}dt=\int \frac{4t}{\sqrt{8-t^2}}dt+\int \frac{7}{\sqrt{8-t^2}}dt=[/m]
[m]=-2\int \frac{d(8-t^2)}{\sqrt{8-t^2}}dt+\int \frac{7}{\sqrt{8-t^2}}dt=-2\cdot2\sqrt{8-t^2}+7arcsin\frac{t}{\sqrt{8}}+C[/m]
осталось вместо t=x+1
