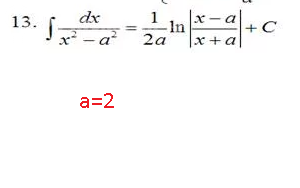Задача 62167 ...
Условие
математика ВУЗ
384
Решение
★
sqrt(x+4)=t
x+4=t^2
x=t^2-4
dx=2tdt
∫ (sqrt(x+4))dx/x= ∫ t*2tdt/(t^2-4)=2 ∫( t^2-4+4)dt/(t^2-4)=2 ∫ dt+8 ∫ dt/(t^2-4)=
=2t+8*(1/4)ln|(t-2)/(t+2)|+C=
=[b]2sqrt(x+4)+2ln|(sqrt(x+4)-2)/(sqrt(x+4)+2)|+C[/b]
