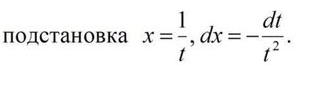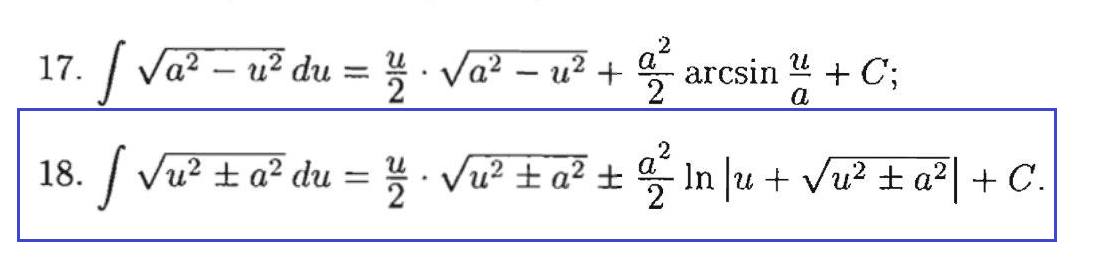Задача 31818 ...
Условие
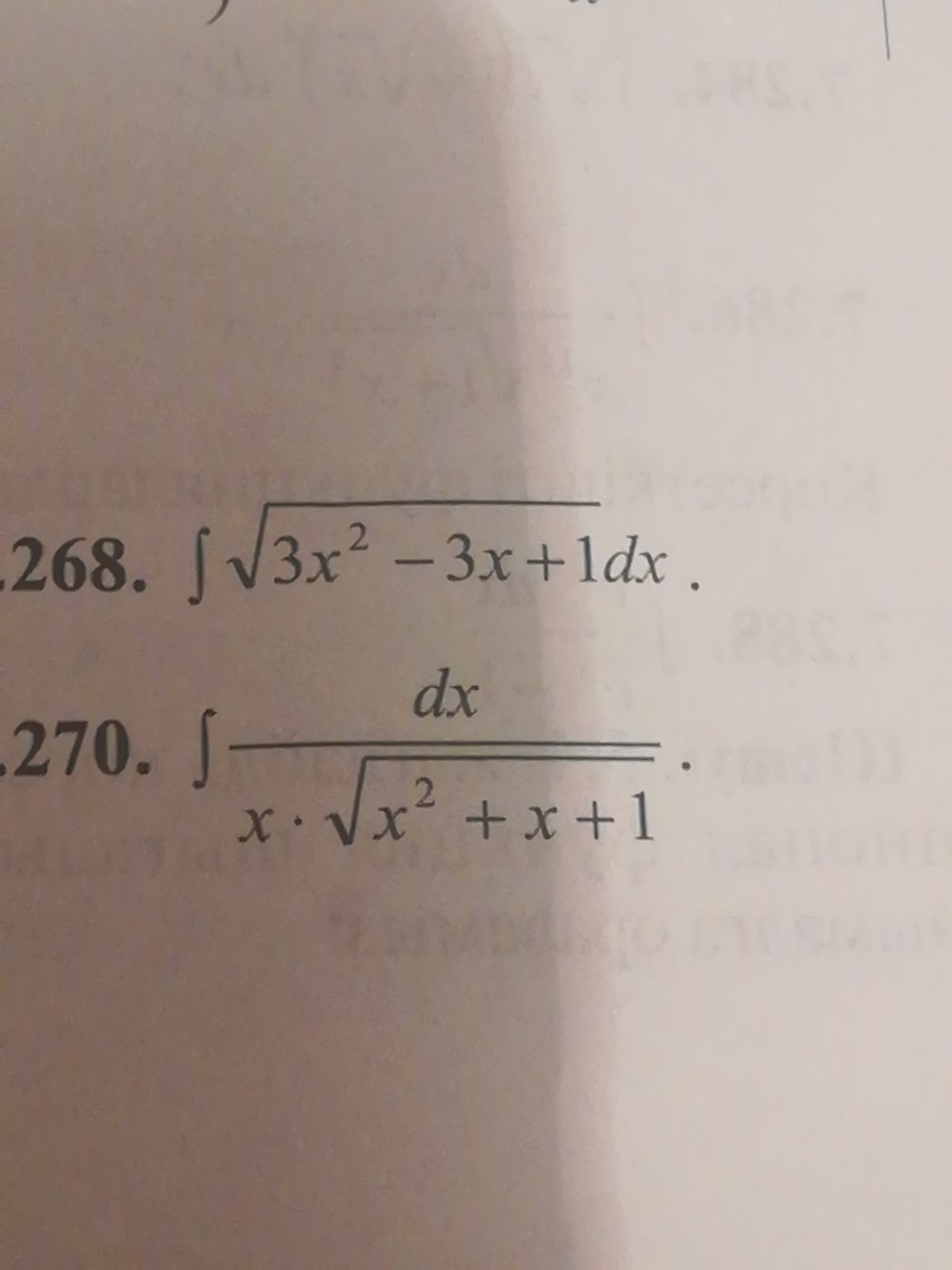
математика ВУЗ
1109
Решение
★
как в 67
∫ sqrt(3x^2-3x+1)dx= sqrt(3)∫ sqrt(x^2-x+(1/3))dx=sqrt(3) ∫ sqrt((x-(1/2))^2-(1/12))dx=
x-(1/2)=u
du=dx
=sqrt(3)*∫ sqrt(u^2-(1/12))du= табличный интеграл, формула 18
=sqrt(3)((1/2)u*sqrt(u^2-(1/24)ln|u+sqrt(u^2-(1/12))|+C=
=(sqrt(3)/2)*(x-(1/2))*sqrt(x^2-x+(1/3))-(sqrt(3)/24)*ln|(x-(1/2))+sqrt(x^2-x+(1/3))|+C
69
Подстановка. См. приложение
= - ∫ dt/(t^2+t+1)= - ∫ dt/sqrt((t+(1/2))^2+(3/4))=табличный интеграл формула 14 - "длинный" логарифм
=-ln|t+(1/2)+sqrt(t^2+t+1)|+C=
=-ln|(1/x)+(1/2)+sqrt((1/x)^2+(1/x)+1)|+C