Задача 37189 подробное решение...

vk173500291

2019-05-17 19:18:08

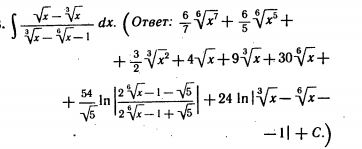
подробное решение

sova

2019-05-17 19:49:17

★

Замена переменной

x=t^6
dx=6t^5dt

sqrt(x)=t^3
∛x=t^2

тогда данный интеграл сводится к интегралу от дроби

∫ (t^3-t^2)*6t^5dt/(t^2-t-1)

Дробь неправильная.

=6 ∫ t^8-t^7)dt/(t^2-t-1)=

=6 ∫ (t^6+t^4+t^3+2t^2+3t+5 + [b](8t+5/(t^2-t-1)[/b])dt=

=6 ∫ (t^6+t^4+t^3+2t^2+3t+5 + [b](8t-4+9/(t^2-t-1)[/b])dt=

=(6t^7/7)+(6t^5/5)+(6t^4/4)+(12t^3/3)+(18t^2/2)+30t+24ln|t^2-t-1|+

54/(2*sqrt(5/4)) ln|(t-1/2-sqrt(5)/2)/(t-1/2+sqrt(5)/2)|+C=

=(6t^7/7)+(6t^5/5)+(6t^4/4)+(12t^3/3)+(18t^2/2)+30t+24ln|t^2-t-1|+

+54/(sqrt(5)) ln|(2t-1-sqrt(5))/(2t-1+sqrt(5))|+C


Как считаем

∫ [b](8t+5)dt/(t^2-t-1)[/b]=

∫ (8t-4+9)dt/(t^2-t-1)=

=4* ∫ (2t-1)dt/(t^2-t-1) + 9* ∫dt/(t^2-t-1)=

первый интеграл табличный. По формуле ∫ du/u

во втором выделяем полный квадрат в знаменателе=

= 4* ln|t^2-t-1| +9 ∫ dt/(t-(1/2))^2-(5/4))=замена t-(1/2)=u

=4* ln|t^2-t-1|+9 ∫ du/(u^2-(5/4))=

=4ln|t^2-t-1|+9*(1/2sqrt(5/4))ln|(u-sqrt(5/4))/(u+sqrt(5/4))|


Это все надо умножить еще на 6.

Получим тот ответ, который и написан в скобках в приложении к вопросу