Задача 59631 ...
Условие
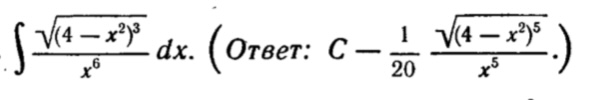
Решение
x=2sint
dx=2costdt
4-x^2=4-4sin^2t=4*(1-sin^2t)=4*cos^2t
sqrt((4-x^2)^3)=(2*cost)^3=8cos^3t
[m]∫\frac{\sqrt{(4-x^2)^3}}{x^6}dx = ∫ \frac{8cos^3t\cdot 2 cost dt}{(2sint)^6}=\frac{1}{4} ∫\frac{cos^4t}{sin^6t}dt= \frac{1}{4} ∫\frac{(1-sin^2t)^2}{sin^6t}dt=[/m]
Тригонометрическая подстановка не привела к табличным интегралам
Значит подстановки Чебышева ( см. скрин)
[m]x^{-6}\cdot \sqrt{(4-x^2)^3}=[/m]
m=-6
n=2
p=3/2
третий случай (m+1)/n + p - целое
Замена
[m]4x^{-2}-1=t^2[/m] ⇒ [m]4x^{-2}=t^2+1[/m]
[m]x^{-2}=\frac{t^2+1}{4}[/m]
[m]x=\frac{2}{\sqrt{t^2+1}}[/m] ⇒
[m]dx=(\frac{2}{\sqrt{t^2+1}})`dt[/m] ...
[m]x^{-6}=\frac{(t^2+1)^3}{4^3}[/m]
