Задача 71999 ...
Условие
∫ sqrt(3-2x-x^2) dx , x+1 = 2sint
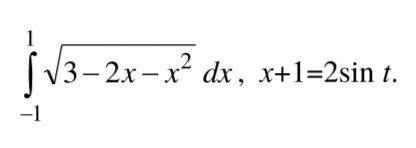
ВУЗ
254
Решение
★
[m]x+1=2sint[/m]
тогда
[m]3-2x-x^2=4-(2sint)^2=4-4sin^2t=4(1-sin^2t)=4cos^2t[/m]
[m]\sqrt{3-2x-x^2}=\sqrt{4cos^2t}=2cost[/m]
[m]x_{1}=-1[/m] ⇒ [m]-1+1=2sint[/m] ⇒ [m]sint=0[/m] ⇒ [m]t_{1}=0[/m]
[m]x_{2}=1[/m] ⇒ [m]1+1=2sint[/m] ⇒ [m]sint=1[/m] ⇒ [m]t_{2}=\frac{π}{2}[/m]
[m]x+1=2sint[/m] ⇒ [m]x=2sint-1[/m]
[m]dx=(2sint-1)`dt[/m]
[m]dx=(2cost)dt[/m]
[m] ∫^{1}_{-1}\sqrt{3-2x-x^2}dx= ∫^{\frac{π}{2}}_{0} 2cost\cdot (2cost)dt=4 ∫^{\frac{π}{2}}_{0} cos^2tdt=4 ∫ \frac{1+cos2t}{2}dt=2(t+\frac{1}{2}sin2t)|^{\frac{π}{2}}_{0}=2(\frac{π}{2}+\frac{1}{2}sinπ)-2(0+0)=π[/m]
