Задача 59234 ...
Условие
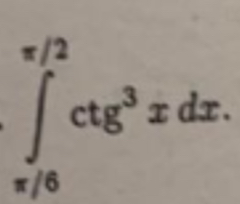
математика колледж
495
Решение
★
∫ ctgx dx= ∫ (cosxdx/sinx)= ∫ d(sinx)/(sinx)= ∫ du/u=ln|u|+C_(1)=ln|sinx|+C_(1)
∫ ctgx *(dx/sin^2x)= ∫ u*(-du)=- ∫ udu=-(u^2/2)+C_(2)=-(1/2)*ctg^2x+C_(2)
