Задача 32039 Помогите решить, но шаг за шагом...
Условие
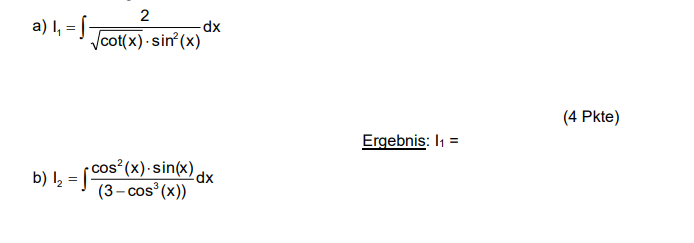
предмет не задан
875
Решение
★
ctgx=t
Берем дифференциалы от обеих частей
d(ctgx)=d(t)
(ctgx)`dx=(t)`*dt
(-1/sin^2x)* dx=dt
(1/sin^2x)dx=-dt
∫ 2dx/(sqrt(cosx)*sin^2x)=-2∫ dt/sqrt(t)=-2*2sqrt(t) + C = -4 sqrt(ctgx) + C
б)а) Замена переменной:
3-cos^3x=t
Берем дифференциалы от обеих частей
d(3 - cos^3x)=d(t)
(3-cos^3x)`dx=(t)`*dt
(-3cos^2x*(cosx)`)* dx=dt
(-3cos^2x*(-sinx) dx=dt
3cos^2x*sinxdx=dt
cos^2x*sinxdx= dt/3
∫cos^2x*sinxdx/(3-cos^3x)=(1/3)∫ dt/t=(1/3)ln|t| + C = (1/3)ln|3-cos^3x| + C
