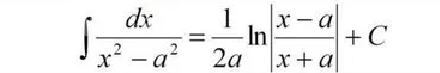Задача 63200 ...
Условие
[block] ∫ (dx)/(4cosx+sinx)[/block]
Решение
(см скрин 1)
Тогда интеграл принимает вид:
[m] ∫ \frac{\frac{2dt}{1+t^2}}{4\cdot \frac{1-t^2}{1+t^2}+\frac{2t}{1+t^2}}= ∫\frac{2dt}{4-4t^2+2t}=∫\frac{dt}{2-2t^2+t}=-∫\frac{dt}{2t^2-t-2} [/m]
Получили интеграл, содержащий квадратный трехчлен.
Выделяем полный квадрат
[m]2t^2-t-2=2(t^2-\frac{1}{2}t-1)=2(t^2-2\cdot \frac{1}{4}+(\frac{1}{4})^2-(\frac{1}{4})^2-1)=[/m]
[m]=2\cdot ((t-\frac{1}{4})^2-\frac{17}{16})[/m]
[m]∫\frac{dt}{2-2t^2+t}= -\frac{1}{2}∫\frac{dt}{(t-\frac{1}{4})^2-\frac{17}{16}} [/m]
Табличный интеграл ( см. скрин 2)
[m] a^2=\frac{17}{16} [/m] ⇒[m] a=\frac{\sqrt{17}}{4} [/m]
[m]x=t-\frac{1}{4}[/m]
[m]=- \frac{1}{2}\cdot \frac{1}{2\frac{\sqrt{17}}{4}}ln|\frac{\frac{(t-\frac{1}{4})-\sqrt{17}}{4}}{(t-\frac{1}{4})+\frac{\sqrt{17}}{4}}| + C[/m]
где
t= tg (x/2)
[m]=- \frac{1}{\sqrt{17}}ln|\frac{4tg\frac{x}{2}-1-\sqrt{17}}{4tg \frac{x}{2}-1+\sqrt{17}}| + C[/m] - это ответ