Задача 37938 ...
Условие
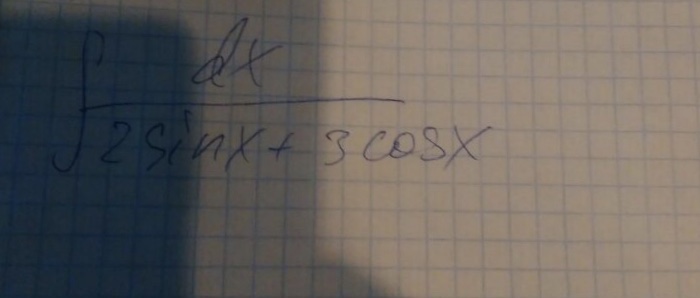
математика ВУЗ
2334
Все решения
tg(x/2)=t
x/2= arctgt
x=2arctgt
dx=2dt/(1+t^2)
sinx=2t/(1+t^2)
cosx=(1-t^2)/*(1+t^2)
∫ dx/(2sinx+3cosx)= ∫ 2dt/(4t+3-3t^2)=(-2/3) ∫ dt/(t^2-(4/3)t+1)=
выделяем полный квадрат
t^2-2*(2/3)t+(4/9)-(4/9)+1=((t-(2/3))^2+(5/9)
=(-2/3)*(1/sqrt(5/9)) arctg (t/sqrt(5/9))+C=
= [b](-2/sqrt(5)) arctg (3tg(x/2))/sqrt(5) +C[/b]

