Задача 31857 Срочно 10 мин осталось помогите пжл...
Условие
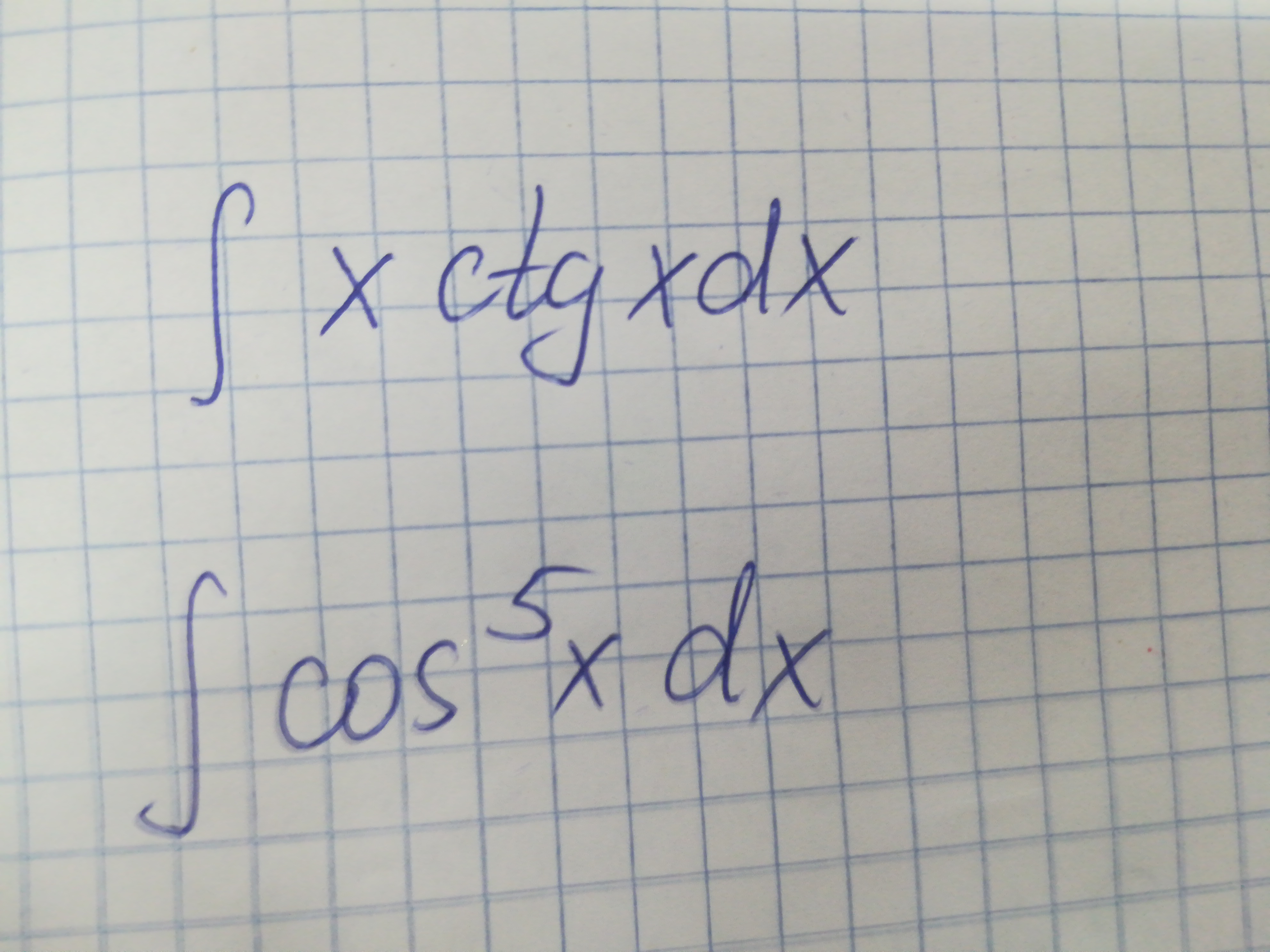
предмет не задан
983
Решение
★
u=x
dv=ctg^2xdx
du=dx
v= ∫ ctg^2xdx= ∫ cos^2xdx/sin^2x= ∫ (1-sin^2x)dx/sin^2x=
= ∫ (dx/sin^2x)- ∫dx= -ctgx - x
∫ udv= u*v- ∫ v*du= x*(-ctgx -x) - ∫ (-ctgx -x)dx=
=-xctgx - x^2 + ∫ ctgxdx + ∫xdx=
=-xctgx - x^2 + ∫ (cosxdx/sinx)+ ∫xdx=
=-xctgx - x^2 +ln|sinx|+ (x^2/2)+C=
=-xctgx +ln|sinx| - (x^2/2)+C
2)
∫ сos^4x*cosxdx= ∫ (cos^2x)^2*cosxdx= ∫ (1-sin^2x)^2*cosxdx=
= ∫ (1-2sin^2x+sin^4x)* cosxdx=
замена
sinx=t
cosxdx=dt
= ∫ (1-2t^2+t^4)dt= t-(2t^3/3)+(t^5/5) + C =
=sinx - (2/3)sin^3x+(1/5) sin^5x+C

