Задача 64172 Необходимо найти объем фигуры...
Условие

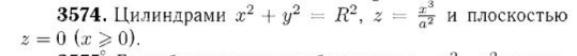
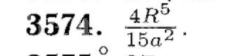
Решение
[m] D: x^2+y^2 ≤ R^2[/m] - круг
Переходим к полярным координатам
[m]x= ρ cos θ [/m]
[m]y= ρ sin θ [/m]
[m]x^2+y^2=( ρ cos θ)^2+(ρ sin θ)^2= ρ ^2(cos^2 θ +sin^2 θ )= ρ^2 [/m]
Тогда уравнение окружности принимает вид
[m] ρ=R[/m]
x ≥ 0 ⇒
[m]-\frac{π}{2}≤ θ ≤\frac{π}{2}[/m]
[m]0 ≤ ρ ≤ R[/m]
[m]dxdy= ρ d ρ dθ[/m] , так как модуль якобиана равен [m] ρ[/m]
[m]V= ∫_{-\frac{π}{2}}^{\frac{π}{2}} ∫ _{0}^{R}\frac{ (ρ cos θ)^3}{a^2} ρ d ρ dθ=\frac{1}{a^2}∫_{-\frac{π}{2}}^{\frac{π}{2}} cos^3 θ (∫ _{0}^{R} ρ^4d ρ)d θ= [/m]
[m]=\frac{1}{a^2}∫_{-\frac{π}{2}}^{\frac{π}{2}} cos^2 θ\cdot cos θ (\frac{ ρ ^5}{5})|_{0}^{R})d θ =[/m]
[m]=\frac{R^5}{5a^2}∫_{-\frac{π}{2}}^{\frac{π}{2}} (1-sin^2 θ)\cdot cos θ d θ =\frac{R^5}{5a^2}∫_{-\frac{π}{2}}^{\frac{π}{2}}(cos θ -sin^2 θ\cdot cos θ ) d θ= [/m]
[m]=\frac{R^5}{5a^2}(sin θ -\frac{sin^3 θ }{3})|_{-\frac{π}{2}}^{\frac{π}{2}}=\frac{R^5}{5a^2}(sin\frac{π}{2} -\frac{sin^3 \frac{π}{2} }{3}-sin(-\frac{π}{2})+\frac{sin^3 (-\frac{π}{2}) }{3})=[/m]
[m]=\frac{R^5}{5a^2}\cdot (2-\frac{2}{3})[/m]
