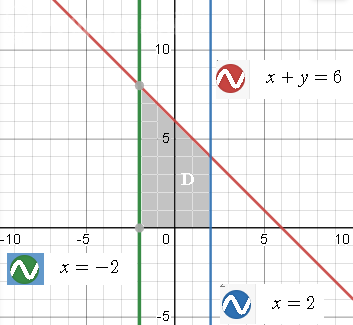Задача 64872 Вычислить объем тела, ограниченного...

Сергей_92688465

29 мая 2022 г. в 12:19

Вычислить объем тела, ограниченного данными поверхностями:
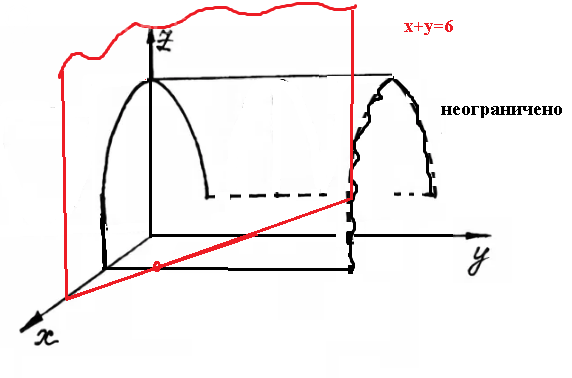
z = 0; z = 4 – x²; y = 0; x + y = 6.

exponenta

29 мая 2022 г. в 18:49

★

z=4–x² – параболический цилиндр с образующими, параллельными оси Оу

z=0 – плоскость хОу, ограничивает тело снизу

Плоскость z=0 пересекается с поверхностью z=4–x² по прямым

4–x²=0 ⇒ x=–2 или x=2

y=0 – плоскость хОz, ограничивает тело слева.


Эту неограниченную справа поверхность пересекает плоскость х+y=6

Поэтому разбираемся, какова область D и какая поверхность ограничивает тело сверху


D см. рис. 2

z=4–x² – ограничивает тело сверху, проекцией на плоскость хОу является область D

D: –2 ≤ x ≤ 2

0 ≤ y ≤ 6–x


[m]V= ∫ ∫_{D} (4-x^2)dxdy= ∫ _{-2}^{2}(∫ _{0}^{6-x} (4-x^2)dy) dx=∫ _{-2}^{2}(4y-x^2y)| _{0}^{6-x} dx=∫ _{-2}^{2}(4(6-x)-x^2(6-x))dx=[/m]

[m]=∫ _{-2}^{2}(24-4x-6x^2+x^3)dx=(24x-2x^2-2x^3+\frac{x^4}{4})| _{-2}^{2}=...[/m]