Задача 35605 Пожалуйста помогите решить примеры от 1...
Условие
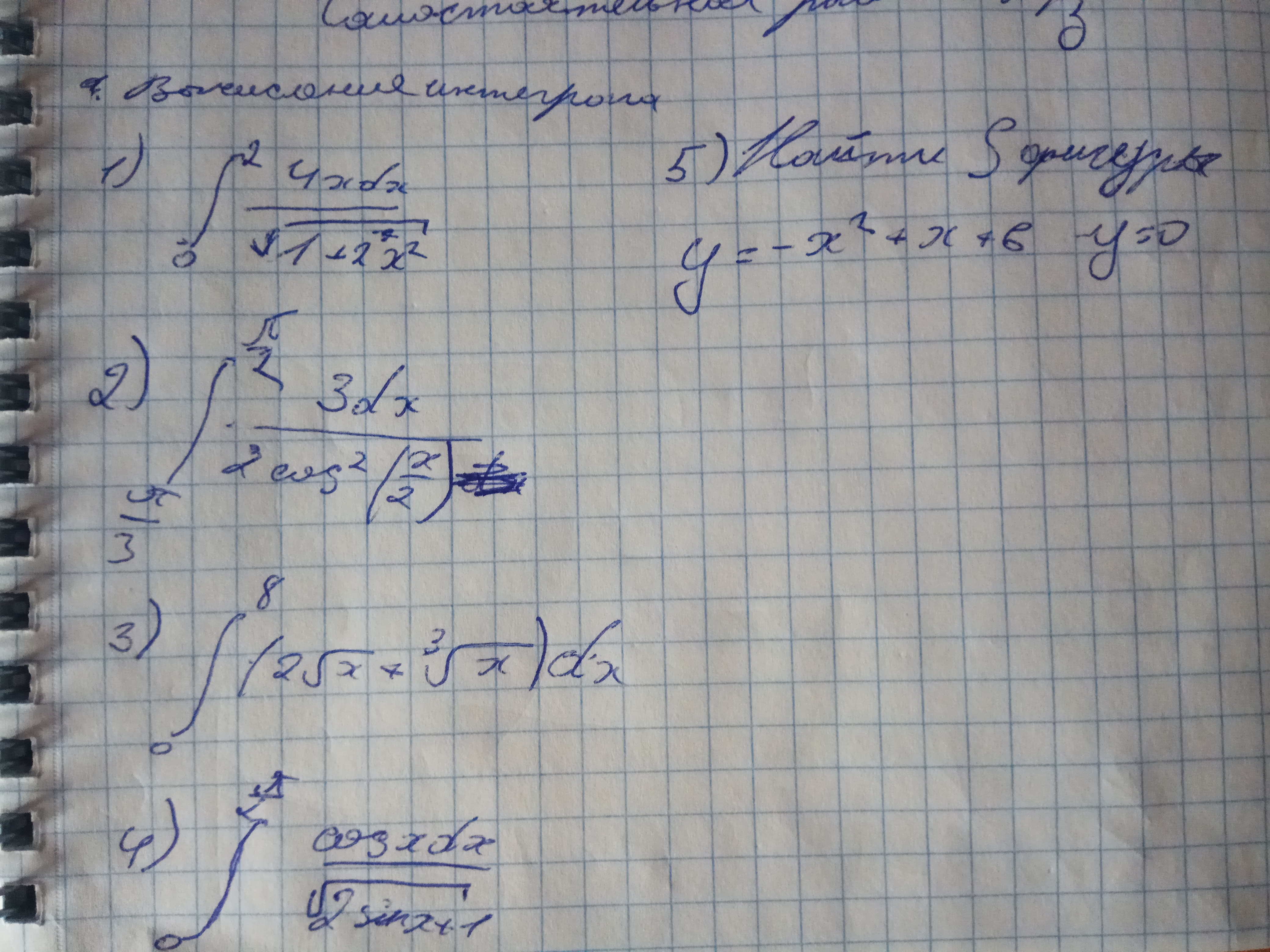
предмет не задан
990
Решение
★
2) =3tg(x/2)|^(π/2)-(π/3)=3tg(π/4)-3tg(π/6)=3-sqrt(3)
3) =(2x^(3/2)/(3/2)+x^(4/3)/(4/3))|^(8)/0=(4/3)*8^(3/2)+(3/4)*8^(4/3)=
=(4/3)*16sqrt(2) +(3/4)*2^(4)=64sqrt(2)/3 +12
4) =(1/2)*2sqrt(2sinx+1)|^(π/2)_(0)=sqrt(2+1)-sqrt(0+1)=sqrt(3)-1
5)
S= ∫^(3) _(-2)(-x^2+x+6)dx=(-x^3/3)|^(3)_(-2)+(x^2/2)|^(3)_(-2)+(6x)|^(3)_(-2)=-9+(8/3)+(9/2)-2+18+12=cчитайте