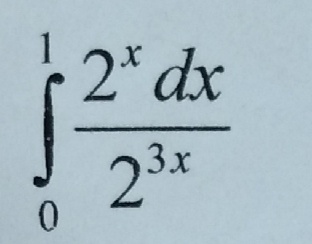Вычисление

Вычислить не определенные интегралы

5
∫√5x + 2dx
-2

Вычислить не определенные интегралы

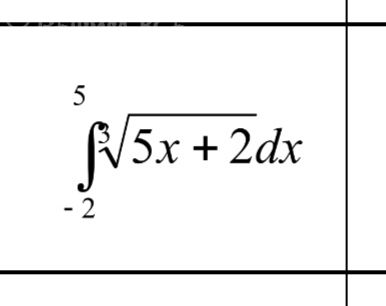
∫ from -7 to 0 ( dx / √(4 - 3x) )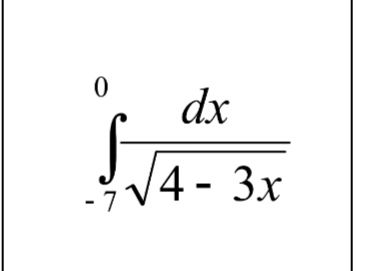

4. Вычислить не определенные интегралы

π/4 ∫ (1 + 5tgx)/cos² x dx π/6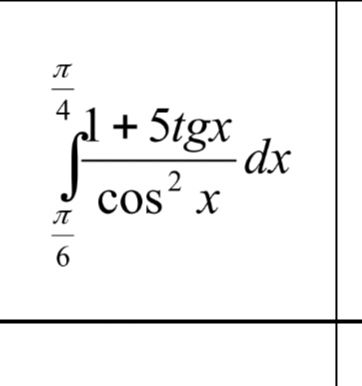

5.Вычислить не определенные интегралы

1
∫(e^x - 1)^(10) · e^x dx
0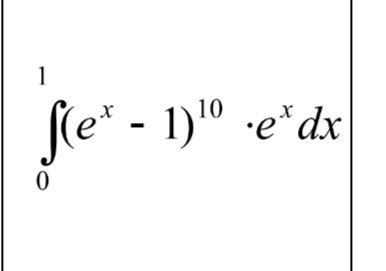

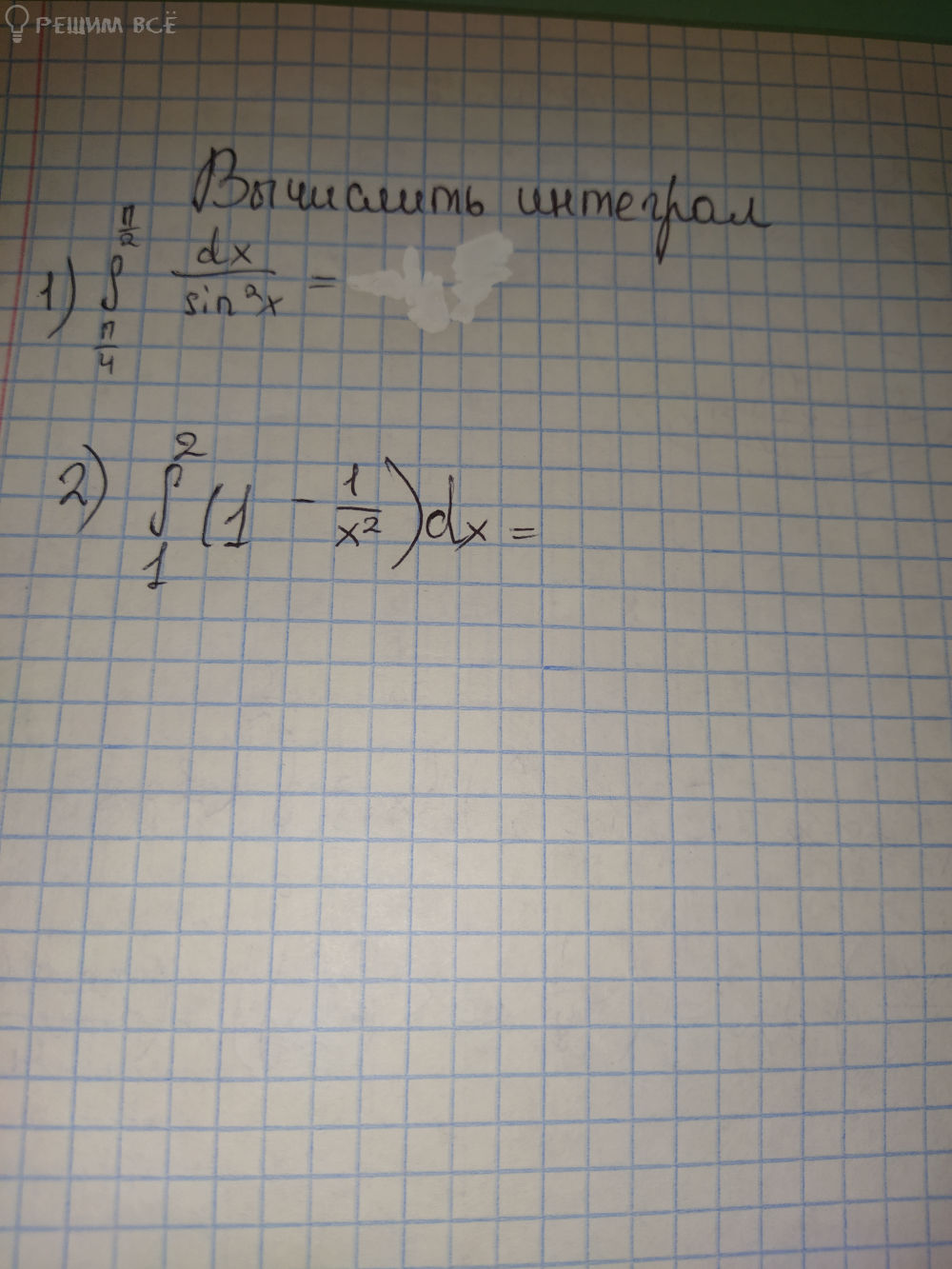
Нужно вычислить интеграл. Есть кто понимает?

Вычислите интеграл 4∫2 x^3dx

1. ∫(от -2 до 1) (x^2-4x+4) dx
2.∫(от 0 до π) sin x/4 dx

∫(от а до 1) dx/(x-4)^2=4/21.

Вычислить интеграл по определению
2,5
∫ (2х+1)^2dx
1

Вычислить определенный интеграл.

∫ от -1 до 1 (x⁵ / (x + 2)) dx

Вычислить определенные интегралы
Вариант 3.6

3. Вычислите определенный интеграл:

∫[от 0,5 до 3] √(2x + 3) dx

∫[от -1 до 1] (4xs + 1)^3 dx

∫[от 2 до 1] (3x^2 - 4x - 1) dx

∫[от 0 до π] cos^2 x sin x dx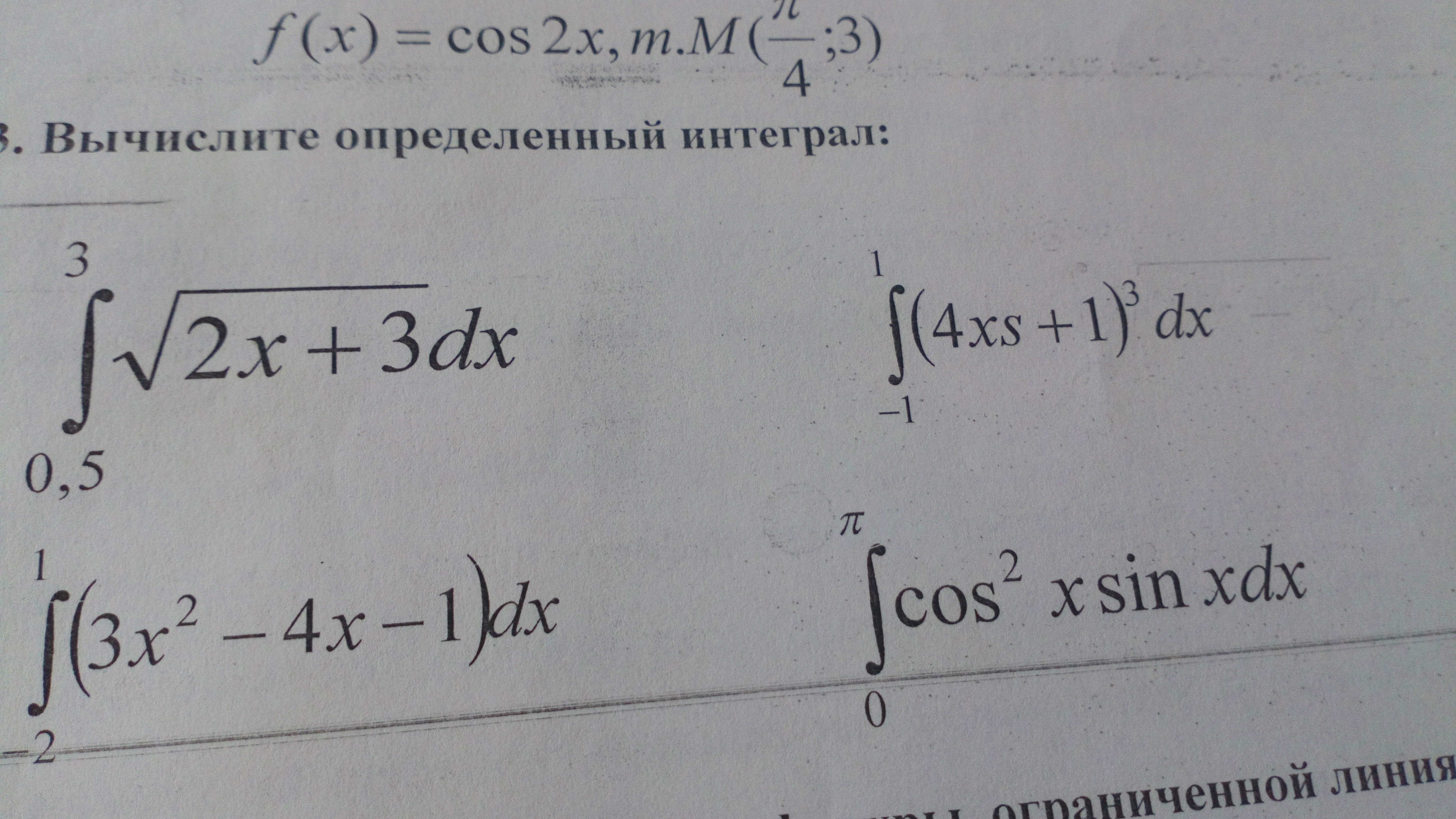

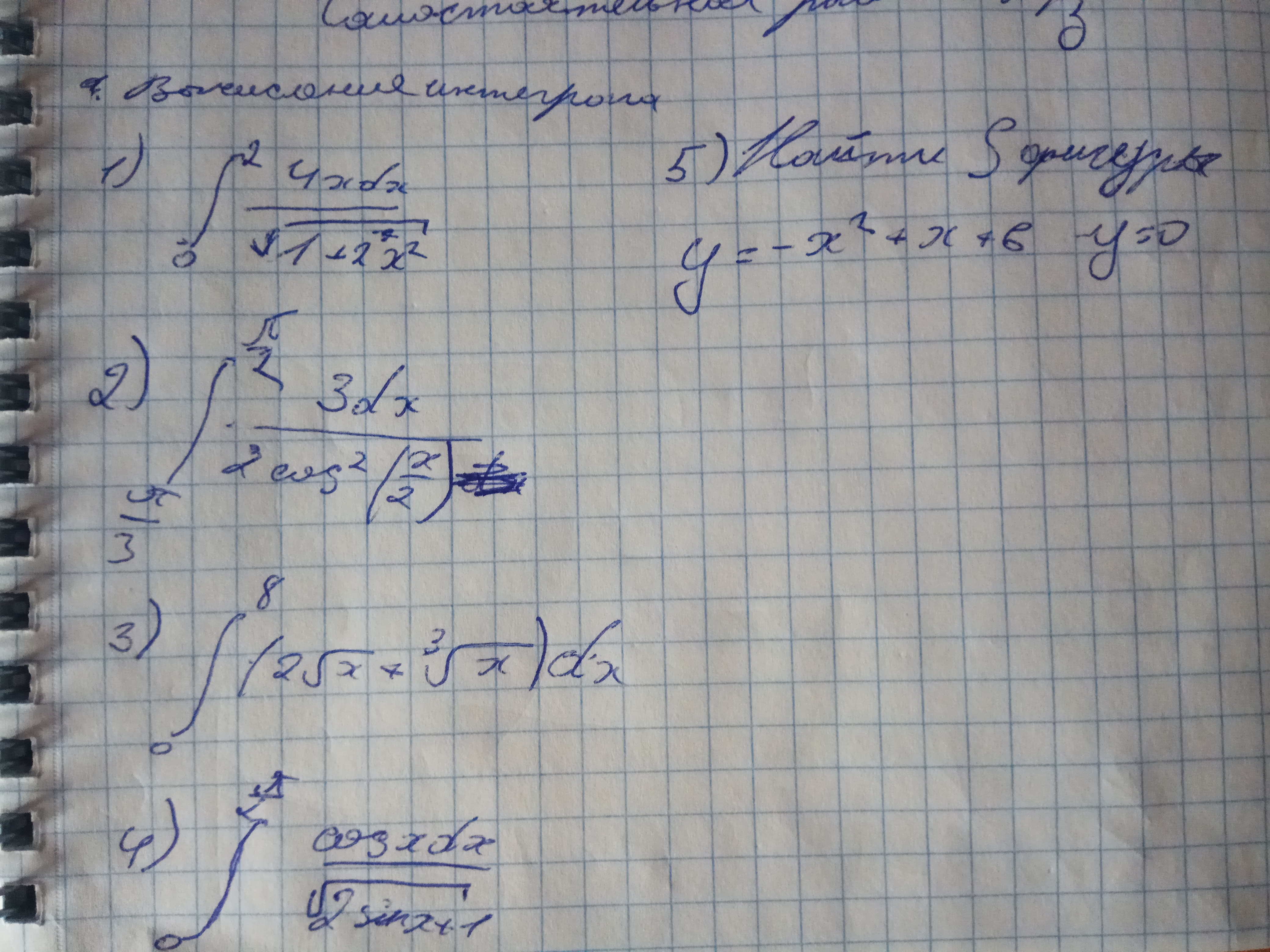
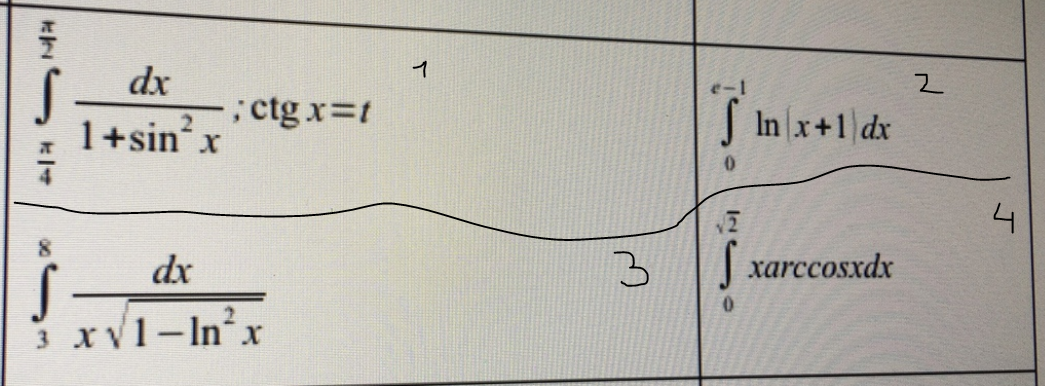
Пожалуйста помогите решить примеры от 1 до 5

Решите,пожалуйста,хотя бы часть.
Первое изображение: 1 столб(1 и 3 пример) решать с заменой переменной,2 столб(2 и 4 пример) решать по частям
Второе изображение(5.12) просто вычислить интегралы во всех столбцах

Вычислить определенный интеграл с точностью до двух знаков после запятой

Вычислить определённый интеграл:
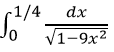
a) ∫[0, π] 3 cos x dx
b) ∫[1, 9] (dx / (x√x))

π/3
∫ (x sin x / cos³ x) dx
0

Вычислить определённые интегралы. Часть 2. Задание 2,3

1. Вычислите log(√3) 5 · log(25) 6 · log6 27 .

2. Найдите значение выражения ∫ ...

1.Найдите указанные неопределенные интегралы.
2.Вычислите указанный определенный интеграл, используя
формулу Ньютона–Лейбница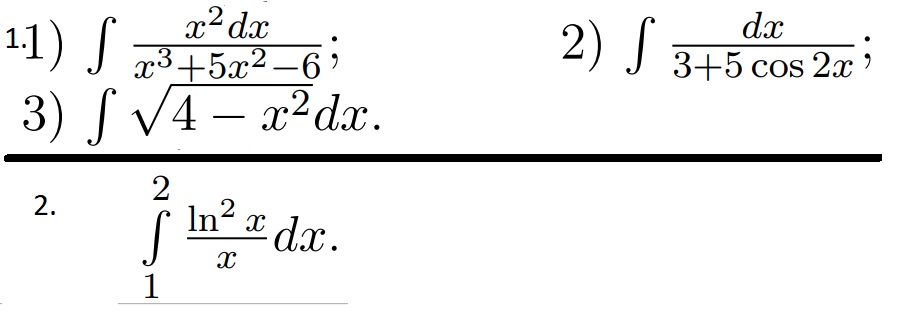

1-найдите определенные интегралы
2-вычислите площадь фигуры ограниченными линиями

Вычислить определенный интеграл

вычислить определенный интеграл

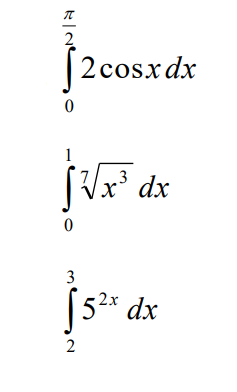
∫ от -1 до 2 от (x * (2/9) * (x + 1)) dx =

Помогите пожалуйста! Вычислить несобственный интеграл или доказать его расходимость

∫₀² 5 · ³√(x - 2)² dx

∫₀¹ 6x dx / (x² - 1)³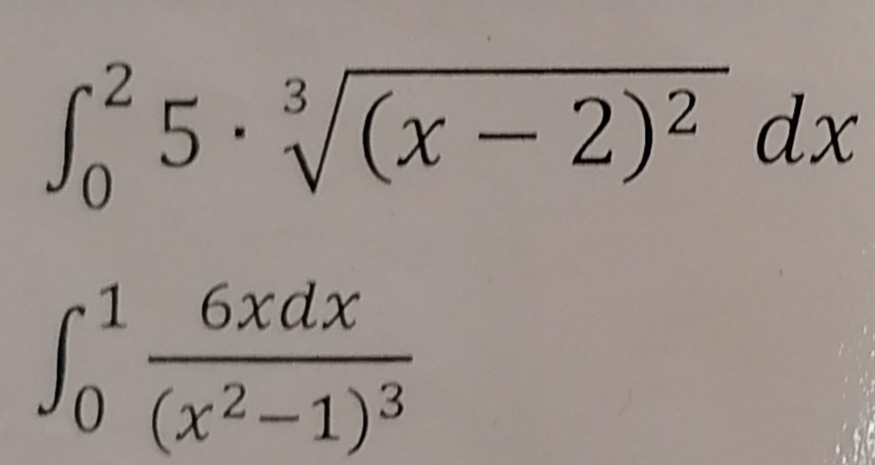

Используя геометрический смысл определенного интеграла, вычислите

∫ (от -2 до 0) (1/Pi) (4-x^2)dx

Вычислите интеграл:
∫ cos² (x + η/3) - sin² (x + η/3) dx.

π/2
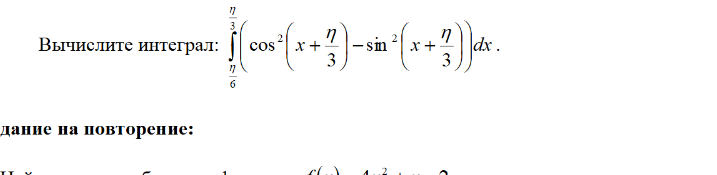
∫ (dx / cos² (4x))
0

определленный интеграл∫4 9 √x /√x－ 1
dx

∫ (2╱2.5) dx / ((2x - 4)^(1/2))

∫[ (-0.5) to (0)] [(2x + 1)^(1/2) - 6(2x + 1)^(2/3)] / (2x + 1)^(2/3) dx

1
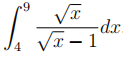
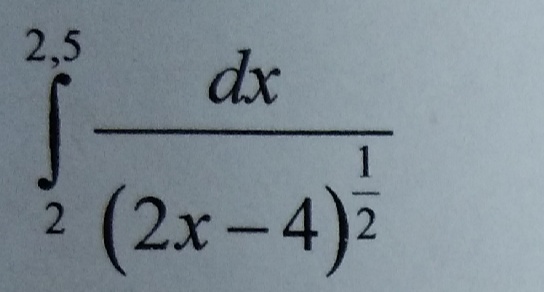
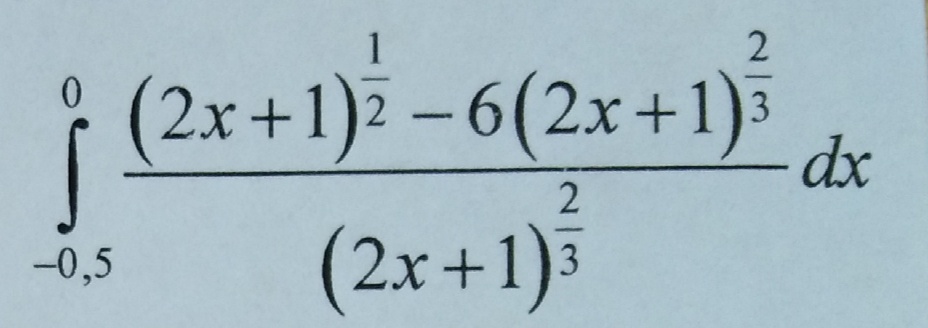
∫ (2^x / 2^(3x)) dx
0

Вычислить определенные интегралы с точностью до двух знаков после запятой