Задача 55360 1-найдите определенные...

5fa27702ff76d766b7a08bbd

06.11.2020 17:41:15

1-найдите определенные интегралы
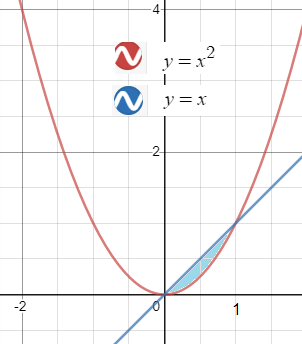
2-вычислите площадь фигуры ограниченными линиями

5f3ea7e3faf909182968ddd9

06.11.2020 18:13:09

★

[m] ∫^{\sqrt{3}}_{1} \frac{32x}{(x^2+1)^5}dx=16∫^{\sqrt{3}}_{1} \frac{2xdx}{(x^2+1)^5}dx=16∫^{\sqrt{3}}_{1} ∫ (x^2+1)^{-5}d(x^2+1)=[/m]

[m]=16\cdot \frac{(x^2+1)^{-5+1}}{(-5+1)}|^{\sqrt{3}}_{1}=-4\cdot \frac{1}{(x^2+1)^{4}}|^{\sqrt{3}}_{1}=-4\cdot (\frac{1}{(\sqrt{3})^2+1)^{4}}-\frac{1}{(1)^2+1)^{4}})=...[/m]

считайте.

[m] ∫^{3}_{1}(x^2-2x)dx=(\frac{x^3}{3}-x^2)|^{3}_{1}=\frac{3^3}{3}-3^2)-\frac{1^3}{3}-1^2)=...[/m]считайте.


[m]S= ∫^{1}_{0}(x-x^2)dx =(\frac{x^2}{2}-\frac{x^3}{3})^{1}_{0}=(\frac{1^2}{2}-\frac{1^3}{3})-0=\frac{1}{6}[/m]