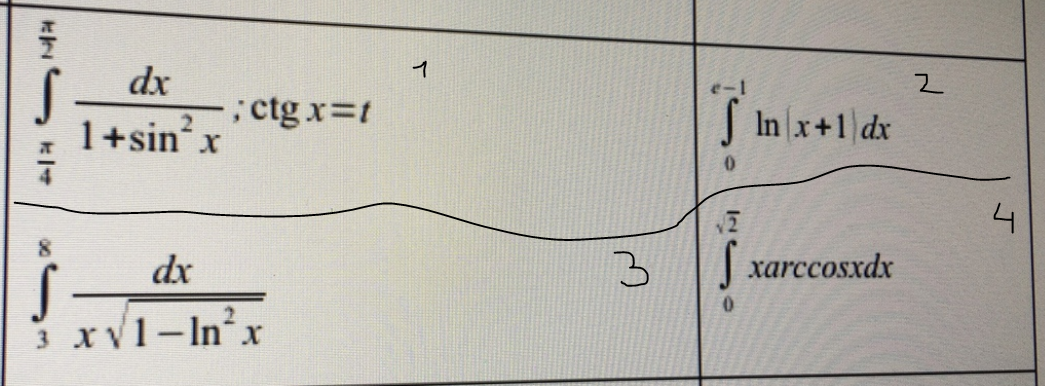
Задача 37702 Решите,пожалуйста,хотя бы часть. Первое...

uuyfcnz123

2019-05-28 18:50:51

Решите,пожалуйста,хотя бы часть.
Первое изображение: 1 столб(1 и 3 пример) решать с заменой переменной,2 столб(2 и 4 пример) решать по частям
Второе изображение(5.12) просто вычислить интегралы во всех столбцах

sova

2019-05-28 21:47:40

★

1.
Формулы тригонометрии:

1+ctg^2x=1/sin^2x ⇒ sin^2x=1/*1+ctg^2x)

1+sin^2x=1+(1/(1+ctg^2x))=(1+ctg^2x+1)/ctg^2x=(2+ctg^2x)/ctg^2x

1/(1+sin^2x)=ctg^2x/(2+ctg^2x)

Замена
ctgx=t ⇒ x= arcctgt

dx=-1/(1+t^2)

Неопределенный интеграл

∫ dx/(1+sin^2x)= -∫ t^2dt/(2+t^2)*(1+t^2) - это интеграл от дроби.
Дробь нужно разложить на две дроби со знаменателями
(2+t^2) и (1+t^2)

- t^2/(2+t^2)*(1+t^2)= 1/(2+t^2) - 1/(1+t^2)

∫ dx/(1+sin^2x)= -∫ t^2dt/(2+t^2)*(1+t^2) =

=∫dt/(2+t^2)-∫dt/(1+t^2)=

=(1/sqrt(2))(- arcctgt/sqrt(2)) +arcctgt=

[b](1/sqrt(2))(- arcctg(x/sqrt(2))) +x[/b]


По формуле Ньютона-Лейбница

∫ ^(π/2)_(π/4)dx/(1+sin^2x)= ([b](1/sqrt(2))(- arcctg(x/sqrt(2))) +x[/b])|^(π/2)_(π/4)


3.

lnx=t
dx/x=dt

Подведение под дифференциал избавит от смены пределов
интегрирования


∫ ^(8)_(3)d(lnx)/sqrt(1-(lnx)^2)=

=arcsin(lnx)|^(8)_(3)= [b]arcsin(ln8)-arcsin(ln3)[/b]


4.

u=arccosx
dv=xdx
du=-1/(sqrt(1-x^2)

v=x^2/2

=((x^2*arccosx)/2)|^(π/2)_(0) - (1/2)* ∫ ^(π/2)_(0) (-x^2dx)/sqrt(1-x^2)=

=((x^2*arccosx)/2)|^(π/2)_(0) - (1/2)* ∫ ^(π/2)_(0) (1-x^2+1)dx/sqrt(1-x^2)=

((x^2*arccosx)/2)|^(π/2)_(0) - (1/2)* ∫ ^(π/2)_(0) sqrt(1-x^2)dx
- (1/2)∫ ^(π/2)_(0)dx/sqrt(1-x^2)=


2.
на [0; e-1]

x+1 >0
|x+1|=x+1

u=ln(x+1)
du=dx/(x+1)

dv=dx

v=x

=х*ln(x+1)|^(e-1)_(0) - ∫^(e-1)_(0) xdx/(x+1)=


=х*ln(x+1)|^(e-1)_(0) - ∫^(e-1)_(0) (x+1-1)dx/(x+1)=

=х*ln(x+1)|^(e-1)_(0) - ∫^(e-1)_(0) (x+1)dx/(x+1)+ ∫^(e-1)_(0) dx/(x+1)=


=х*ln(x+1)|^(e-1)_(0) - ∫^(e-1)_(0)dx+ ∫^(e-1)_(0) dx/(x+1)=

=х*ln(x+1)|^(e-1)_(0) - x|^(e-1)_(0) +ln|x+1||^(e-1)_(0)=