Задача 63419 Вычислить не определенные интегралы...
Условие
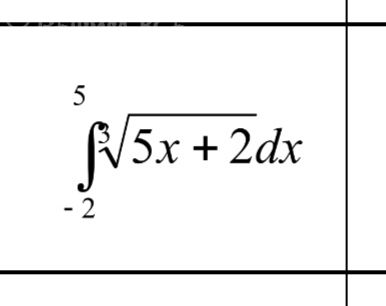
математика колледж
242
Решение
★
[m]dx=\frac{1}{5}d(5x+2)[/m]
[m]∫_{-2} ^{3}\sqrt[3]{5x+2}dx=∫_{-2} ^{3}\sqrt[3]{5x+2}\frac{1}{5}d(5x+2)=\frac{1}{5}∫_{-2} ^{3}\sqrt[3]{5x+2}d(5x+2)=[/m]
формула
[m]∫\sqrt[3]{u}d(u)= ∫u^{\frac{1}{3}}du=\frac{u^{\frac{1}{3}+1}}{\frac{1}{3}+1} =\frac{u^{\frac{4}{3}}}{\frac{1}{3}}[/m]
[m]=\frac{1}{5}\cdot (\frac{(5x+2)^{\frac{4}{3}}}{\frac{4}{3}})|_{-2} ^{3}=\frac{3}{20}((5\cdot 3+2)^{\frac{4}{3}}-(5\cdot (-2)+2)^{\frac{4}{3}})=\frac{3}{20}\cdot \sqrt[3]{17^{4}}-\frac{3}{20}\cdot \sqrt[3]{(-8)^{4}} [/m]
