Задача 33354 Помогите пожалуйста! Вычислить...
Условие
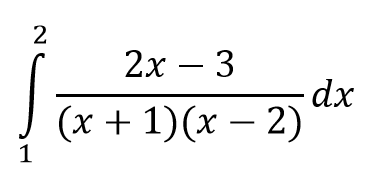
Решение
(2x-3)/((x+1)*(x-2))=A/(x+1) + B/(x-2)
2x-3 =A*(x-2)+B*(x+1)
2x-3=(A+B)x -2A+B
2=A+B
-3=-2A+B
Вычитаем из первого второе
5=3А
А=5/3
В=1/3
Получаем два интеграла
(5/3) ∫^(2) _(1)dx/(x+1)- определенный интеграл, его вычисление приводит нас к числу.
=(5/3)(ln|x+1|)|^(2)_(1)= (5/3) ln 3-(5/3) ln2=(5/3) ln (3/2)
и
(1/3) ∫^(2) _(1)dx/(x-2) - несобственный интеграл 2 рода с особой точкой х=2
По определению
(1/3) ∫^(2) _(1)dx/(x-2)=
=(1/3)lim_(δ→0) ∫^(2-δ)_(1)dx/(x-2)=
=(1/3)lim_(δ→ 0)ln|2-δ-2|-(1/3) ln|1 - 2|=(1/3)lim_(δ→ 0)ln|-δ|= ∞ - 0 =
= ∞
Интеграл расходится
Сумма числа ( первый интеграл) и бесконечности есть бесконечность.
О т в е т. расходится.
Можно не раскладывать подынтегральную функцию на дроби, а раскрыть скобки в знаменателе и выделить полный квадрат.
(х+1)(х-2)=x^2-x-2=(x-(1/2))^2-(9/4)
∫ (2x-3)dx/(x+1)(x-2)= ∫ (2x-3)dx/((x-(1/2)^2-(9/4))
Замена
x-(1/2)=t
x=t+(1/2)
dx=dt
= ∫ (2t-2)dt/(t^2-(9/4))= ∫ (2t)dt/(t^2-(9/4)) - ∫ 2dt/(t^2-(9/4))=
=ln|t^2-(9/4)| -2ln|(t-(3/2))/(t+(3/2))|
...
