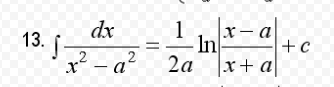Задача 32710 Вычислить определённые интегралы. Часть...

89965026654

2019-01-14 13:35:03

Вычислить определённые интегралы. Часть 2. Задание 2,3

sova

2019-01-14 14:00:49

★

2.
Выделим полный квадрат
x^2+2x=x^2+2x+1-1=(x+1)^2-1
d(x+1)=dx

= ∫ ^(2)_(1)d(x+1)/((x+1)^2-1)=(1/2)ln|(x+1-1)/(x+1+1)|^(2)_(1)=

=(1/2)*(ln(2/4)-ln(1/3))=(1/2)*ln(3/2)

3.
Интегрирование по частям
u=x^2
du=2xdx
dv=x*e^(x^2)dx
v=(1/2)*e^(x^2)
∫x^3*e^(x^2)dx=(x^2/2)*e^(x^2)- ∫x*e^(x^2)dx=

=(x^2/2)*e^(x^2)-(1/2)*e^(x^2).

О т в е т. ∫^(1)_(0)x^3*e^(x^2)dx=((x^2/2)*e^(x^2)-(1/2)*e^(x^2))|^(1)_(0)=

=(e/2)-(e/2)+1/2=1/2.