Задача 35234 ...
Условие
∫[от 0,5 до 3] √(2x + 3) dx
∫[от -1 до 1] (4xs + 1)^3 dx
∫[от 2 до 1] (3x^2 - 4x - 1) dx
∫[от 0 до π] cos^2 x sin x dx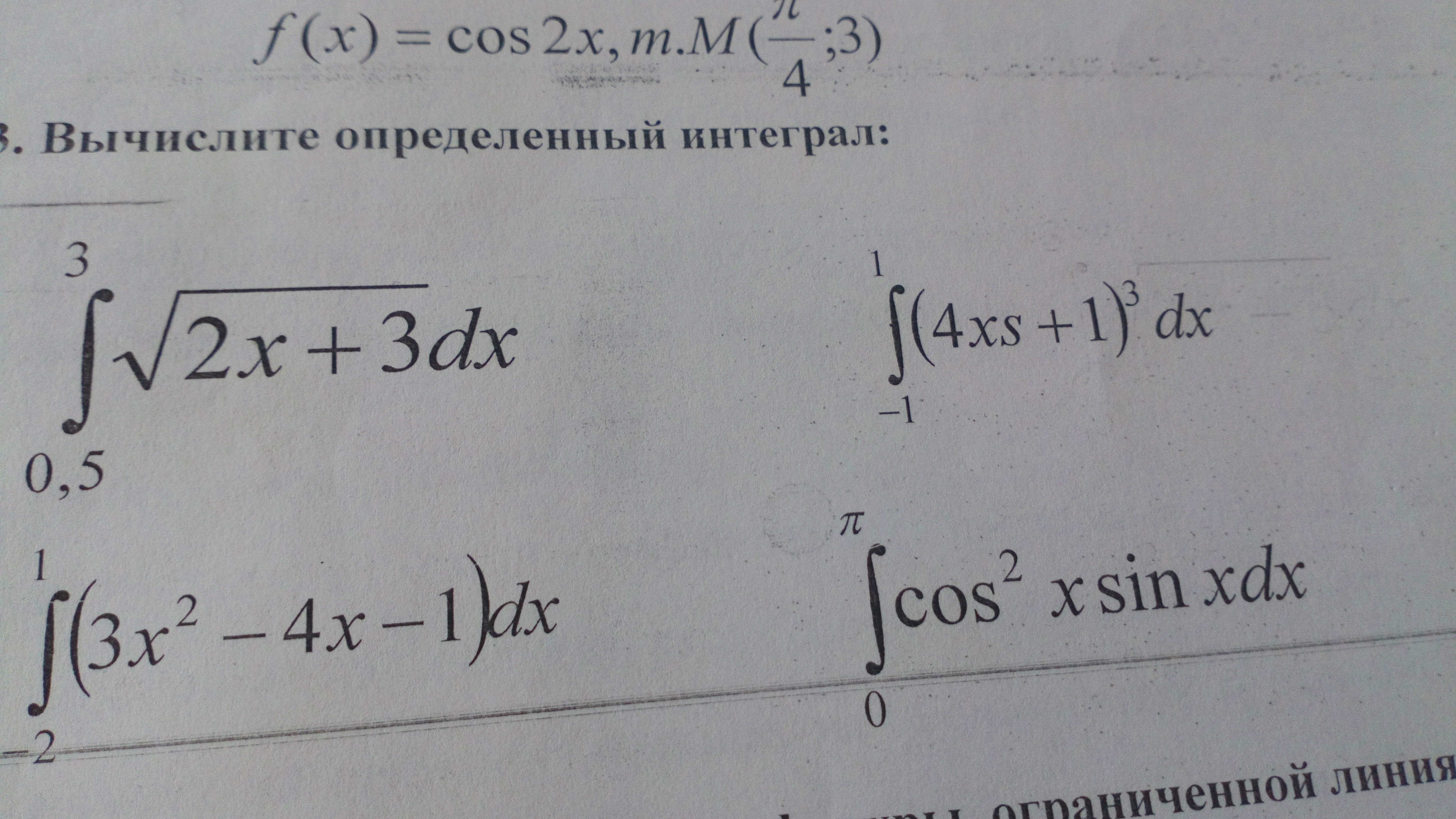
Все решения
=(2x+3)^((1/2)+1)/((1/2)+1)=(2/3)(2x+3)^(3/2)|^(3)_(0,5)=
=(2/3)*(2*3+3)^(3/2) - (2/3)*(2*0,5+3)^(3/2)=
=(2/3)3^3-(2/3)*2^3=(2/3)*(27-8)= [b]38/3[/b]
∫ ^(1)_(-2)(3x^2-4x-1)dx= (x^3-2x^2-x)|^(1)_(-2)=
=(1-2-1)-(-8-8-(-2))= [b]...[/b]
∫ ^(π)_(0)cos^2xsinxdx=∫ ^(π)_(0)cos^2x(-d(cosx))=
= -(cos^3x/3)|^(π)_(0)=-(1/3)*(cos^(3)(π)-cos0)=(-1/3)*(-1-1)= [b]2/3[/b]
∫ ^(1)_(-1)(4xS+1)^3dx=(1/(4S)) ∫ ^(1)_(-1)(4xS+1)^3d(4xS+1)=
=(1/(4S)) *(4xS+1)^4/4|^(1)_(-1)= [b](1/(16S)) *((4S+1)^4-(1-4S)^4)[/b]
