Задача 54968 ...
Условие
∫₀¹ 6x dx / (x² - 1)³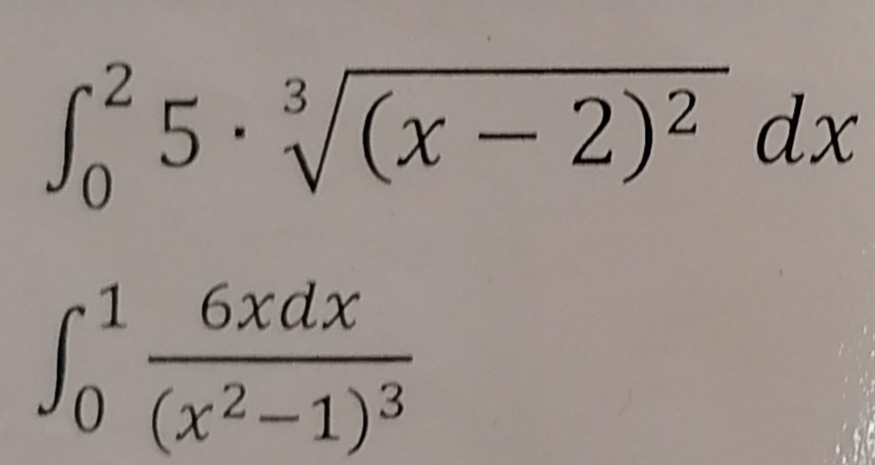
Решение
Неопределенный интеграл [m] \int f (x) dx=F(x)+C[/m] - совокупность первообразных
Определенный интеграл: это предел интегральных сумм.
Определенный и неопределенный [b] связывает[/b] формула:
[m] \int^{b}_{a} f(x)dx=F(x)|^{b}_{a}[/m]- формула Ньютона -Лейбница
[b]Вывод[/b]: чтобы считать [i] определенный[/i] нужно уметь считать [i] неопределенный[/i].
Все правила и и формулы аналогичные( интеграл от суммы равен..., постоянный множитель можно выносить..., таблица интегралов, т.е нахождения первообразных)
и [b] методы[/b] тоже ( аналогичные, но есть особенности, в них-то и надо разобраться)
Одним из таких методов является [b]метод замены переменной[/b]
1) [m]∫ 5\cdot \sqrt[3]{(x-2)^2}dx=[/m]
Постоянный множитель можно выносить за знак интеграла
[m]=5 ∫(x-2)^{\frac{2}{3}}dx= [/m]
применяем метод замены переменной в[i] неопределенном[/i] интеграле:
u=(x-2)
du=(x-2)`dx ⇒ du=dx
получаем
[m]=5\cdot ∫u^{\frac{2}{3}}du= [/m]
а это уже табличный интеграл
[m] ∫ u^{ α }du=\frac{u^{ α+1 }}{α+1}+C[/m]
получим для [m]α =\frac{2}{3} [/m]
[m]=\frac{u^{ \frac{2}{3}+1} }{\frac{2}{3}+1}+C[/m]
обратная замена:
[m] ∫(x-2)^{\frac{2}{3}}dx=\frac{(x-2)^{ \frac{2}{3}+1 }}{\frac{2}{3}+1}+C[/m]
метод замены переменной в [i]определенном[/i] интеграле :
надо поменять пределы интегрирования:
eсли [m] x_{1}=0[/m], то [m] u_{1}=0-2=-2[/m]
eсли [m] x_{2}=2[/m], то [m]u_{2}=2-2=0[/m]
и решение можно записать так:
[m]∫^{2}_{0} 5\cdot \sqrt[3]{(x-2)^2}dx=[/m]
Постоянный множитель можно выносить за знак интеграла
[m] 5\cdot ∫^{2}_{0}(x-2)^{\frac{2}{3}}dx=[/m]
замена переменной:
[m]u=x-2[/m]; [m]du=dx[/m];
eсли [m] x_{1}=0[/m], то [m] u_{1}=0-2=-2[/m]
eсли [m] x_{2}=2[/m], то [m] u_{2}=2-2=0[/m]]
[m]= 5\cdot ∫^{0}_{-2}u^{\frac{2}{3}}du=[/m]
табличный интеграл и формула Ньютона - Лейбница ( и не надо делать обратный переход от переменной[m] u [/m] к [m]x[/m]):
[m]=5\cdot (\frac{u^{ \frac{2}{3}+1 }}{\frac{2}{3}+1})|^{0}_{-2}=[/m]
[m]=5\cdot \frac{3}{5}u^{ \frac{5}{3}}=|^{0}_{-2}= 3\cdot (0-(-2)^{\frac{5}{3}}=3\cdot (-2)\sqrt[3]{-4}=-6\sqrt{-4}[/m]-это ответ.
Но самое интересное в том, что решение этой задачи можно записать еще проще, если не расписывать замену переменной, а применять аналог замены: [red]метод подведения под знак дифференциала [/red]
[m] ∫ f(x)dx[/m]=[метод замены: x=u]=[m] ∫ f(u(x))d(u(x))[/m] →
в обратную сторону это [m] ∫ f(u(x))d(u(x))[/m]= [метод подведения под дифференциал[m]∫ f(x)dx[/m]
Метод основан на том, что[red] в условии таких интегралов[/red] ( а у вас целый столбик их, все на эту тему)
дифференциал новой переменной совпадает с dx или отличается от dx на const
Итак, первый пример:
[red][m]∫^{2}_{0} 5\cdot \sqrt[3]{(x-2)^2}dx=[/m][/red]
Постоянный множитель можно выносить за знак интеграла
[m] 5\cdot ∫^{2}_{0}(x-2)^{\frac{2}{3}}dx=[/m]
и так как
[m]d(x-2)=dx[/m]
[m] =5\cdot ∫^{2}_{0}(x-2)^{\frac{2}{3}}d(x-2)=[/m]
=на этом этапе вводили замену и меняли пределы интегрирования, но можно ничего этого не расписывать:
[m]=5\cdot (\frac{(x-2)^{ \frac{2}{3}+1 }}{\frac{2}{3}+1})|^{2}_{0}=[/m]
[m]=5\cdot \frac{3}{5}(x-2)^{ \frac{5}{3}}|^{2}_{0}= 3\cdot (2-2)^{\frac{5}{3}}-3\cdot(0-2)^{\frac{5}{3}} =[/m]
[red][m]=3\cdot (-2)\sqrt[3]{-4}=-6\sqrt[3]{-4}[/m][/red]
[green]Второй пример:[/green]
Это [b]несобственный интеграл[/b] второго рода,так как в точке х=1 знаменатель обращается в нуль (!)
Поэтому все эти расписывания замены и смены пределов - пустая трата времени.
Решение:
[m] ∫ ^{1 }_{0}\frac{6x dx}{(x^2-1)^3}=lim_{ ε →0} ∫ ^{1- ε }_{0}\frac{6x dx}{(x^2-1)^3}=3\cdot lim_{ ε →0} ∫ ^{1- ε }_{0}(x^2-1)^{-3}(2xdx)=[/m]
так как [m] d(x^2-1)=2xdx[/m]
[m]=3\cdot lim_{ ε →0} ∫ ^{1- ε }_{0}(x^2-1)^{-3}d(x^2-1)=3\cdot lim_{ ε →0} \frac{(x^2-1)^{-3+1}}{-3+1}|^{1- ε }_{0}=3\cdot (-\frac{1}{2}\cdot) lim_{ ε →0} \frac{1}{x^2-1)^2})|^{1- ε }_{0}=-\frac{3}{2}(\frac{1}{(1- ε)^2-1)^{2}}-\frac{1}{0^2-1)^2})= ∞ [/m]
О т в е т. Расходится.
