Задача 35523 Вычислить определенные интегралы Вариант...

priora844

2019-04-08 15:25:50

Вычислить определенные интегралы
Вариант 3.6

sova

2019-04-08 15:47:09

★

а)
замена переменной:
∛1+x=t
1+x=t^3
x=t^3-1
dx=3t^2dt

x=-1 ⇒ t=0
x=0 ⇒ t=1

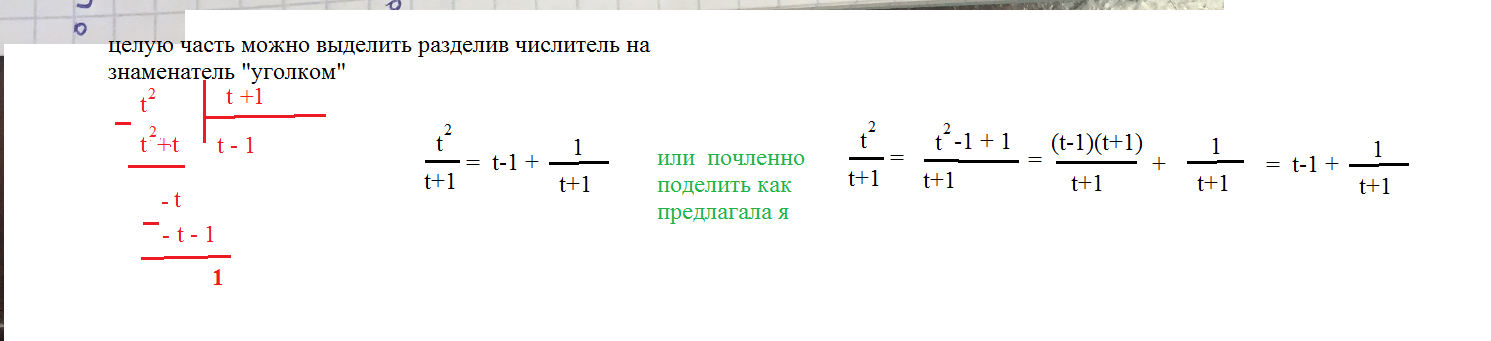
= ∫ ^(1)_(0)3t^2dt/(1+t)=3 ∫ ^(1)_(0) ((t^2-1)+1)dt/(t+1)=


=3 ∫ ^(1)_(0)( (t-1)+(1/(t+1)))dt=3(t^2/2 - t + ln |t+1|)|^(1)_(0)=

=3*((1/2)-1+ln2) - о т в е т.

б)
по частям

u=x ⇒ du=dx
dv=5^(x)dx ⇒ v=5^(x)/ln5

∫ ^(2)_(0) x*5^(x)dx= (x*5^(x)/ln5)|^(2)_(0) - ∫ ^(2)_(0)5^(x)dx/ln5=

=2*5^2/ln5 - (1/ln5)*(5^(x)/ln5)|^(2)_(0)=

=(50/ln5) - (25-1)/(ln5)^2=(50/ln5) - (24)/(ln5)^2 - о т в е т.