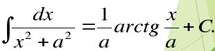Задача 33604 Решить интеграл Dx/(x(5+ln^2x)...

nashipitsina

2019-02-15 13:37:31

Решить интеграл
Dx/(x(5+ln^2x)

sova

2019-02-15 13:41:23

Замена переменной
u=lnx
du=(lnx)`dx
du=(1/x)*dx
получим:
∫ du/(5+u^2)=(1/sqrt(5))*arctg (u/sqrt(5)C=(1/sqrt(5))*arctg (5+ln^2x)/sqrt(5) + C