Задача 35959 ...
Условие
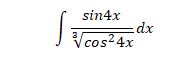
предмет не задан
657
Решение
★
∫ u^(-2/3)du=u^((-2/3)+1)/((-2/3)+1)+C=3∛u + C
u=cos4x
du=(cos4x)`dx
du=-sin4x*(4x)`dx=-4sin4xdx
sin4xdx=(-1/4)du
∫ sin4xdx/∛(cos^24x)=(-1/4) ∫ u^(-2/3)du=(-1/4)*3∛u + C=
=(-3/4)∛(cos4x) + C
