Задача 34157 ...
Условие
2. ∫ sin(1-x^2)x dx
3. ∫ e^x dx / (4+e^(2x))
...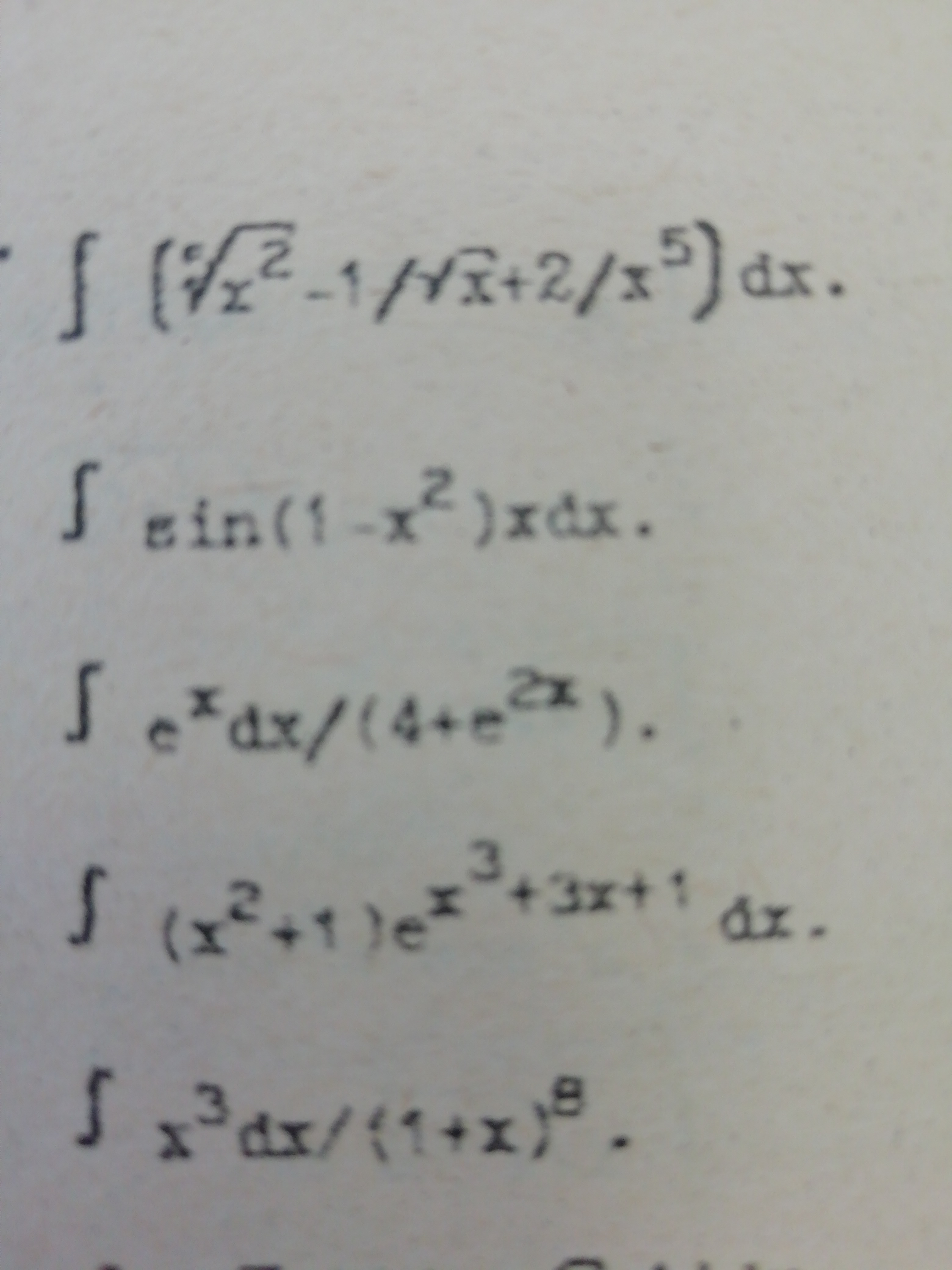
Решение
Замена переменной. Подведение под дифференциал.
1.
Интеграл от суммы равен сумме интегралов.
постоянный множитель можно вынести за знак производной.
Используем свойства степени:
a^(m)/a^(n)=a^(m-n)
a^(-n)=1/a^(n)
Применяем формулу интеграла от степенной функции:
[b] ∫ x^( α )dx=x^( α +1)/( α +1)[/b]
получаем
= ∫ x^(2/5)dx- ∫ x^(-1/2)dx+2 ∫ x^(-5)dx=
=x^((2/5)+1)/((2/5)+1) - x^(-1/2)+1)/((-1/2)+1) +2*x^(-5+1)/(-5+1)+C=
=x^(7/5) / (7/5) - 2x^(1/2) -(1/2)*x^(-4)+C=
= [b](5/7)*x*x^(2/5) - 2sqrt(x) -1/(2x^4) + C[/b].
2.
Табличный интеграл
[b]∫ sinudu = - cosu + C[/b]
Замена переменной
1-x^2=u
-2xdx=du
xdx=(-1/2)du
получаем
∫ sinu(-1/2)du= (-1/2) ∫ sinudu=(-1/2)*(-cosu) + C=(1/2)cosu+C=
= обратная замена=
[b]=(1/2)cos(1-x^2)+ C[/b]
3.
Табличный интеграл
[b] ∫ du/(4+u^2) = (1/2)arctg(u/2) + C[/b]
Замена переменной
e^(x)=u
e^(x)dx=du
получаем
∫ du/(4+u^2) = (1/2)arctg(u/2) + C=
= обратная замена=
= [b](1/2)arctg (e^(x)/2)+ C[/b]
4.
Табличный интеграл
[b] ∫ e^(u)du = e^(u) + C[/b]
Замена переменной
x^3+3x+1=u
d(x^2+3x+1)=du
(x^3+3x+1)`dx=du
(3x+3)dx=du
(x+1)dx=du/3
получаем
∫ e^(u)*(du/3) = (1/3)∫ e^(u)du = (1/3)e^(u)+C
= обратная замена=
= [b](1/3)e^(x^3+3x^2+1)+ C[/b]
5.
Замена переменной
[b]1+x=t[/b]
x=t-1
dx=d(t-1)
dx=(t-1)`*dt
dx=1*dt
[b]dx=dt[/b]
получаем
∫(t-1)^3dt/t^(8)=
формула куба разности:
= ∫ (t^3-3t^2+3t-1)/t^(8)=
почленное деление каждого слагаемого в числителе на знаменатель:
= ∫ (t^3/t^(8) -3*(t^2/t^8)+3*(t/t^8)-(1/t^8))dt=
Интеграл от суммы равен сумме интегралов.
постоянный множитель можно вынести за знак производной.
= ∫ dt/t^(5) -3 ∫ dt/t^(6)+3 ∫ dt/t^(7) - ∫ dt/t^(8)=
Используем свойства степени:
a^(-n)=1/a^(n)
= ∫ t^(-5)dt - 3 ∫ t^(-6)dt +3 ∫ t^(-7)dt - ∫ t^(-8)dt=
Применяем формулу интеграла от степенной функции:
[b] ∫ x^( α )dx=x^( α +1)/( α +1)[/b]
=t^(-4)/(-4) - 3*(t^(-5)/(-5)) +3*(t^(-6)/(-6)) - t^(-7)/(-7)+C=
=(-1/4)*(1/t^4) +(3/5)*(1/t^5)-2*(1/t^6) +(1/7)*(1/t^7)+C=
= обратная замена=
=[b]-1/(4*(x+1)^4) + 3/(5*(x+1)^5)-(2/(x+1)^6) +(1/7(x+1)^7)+C[/b]
