Случайные величины

Два стрелка независимо друг от друга делают по своей мишени 1 выстрел. Найти ряд распределения , функцию распределения и числовые характеристики?

6. Задан закон распределения дискретной случайной величины Х.
Найти:
1) математическое ожидание М(Х);
2) дисперсию D(X);
3) среднее квадратическое отклонение
(х)
;
4) построить многоугольник распределение
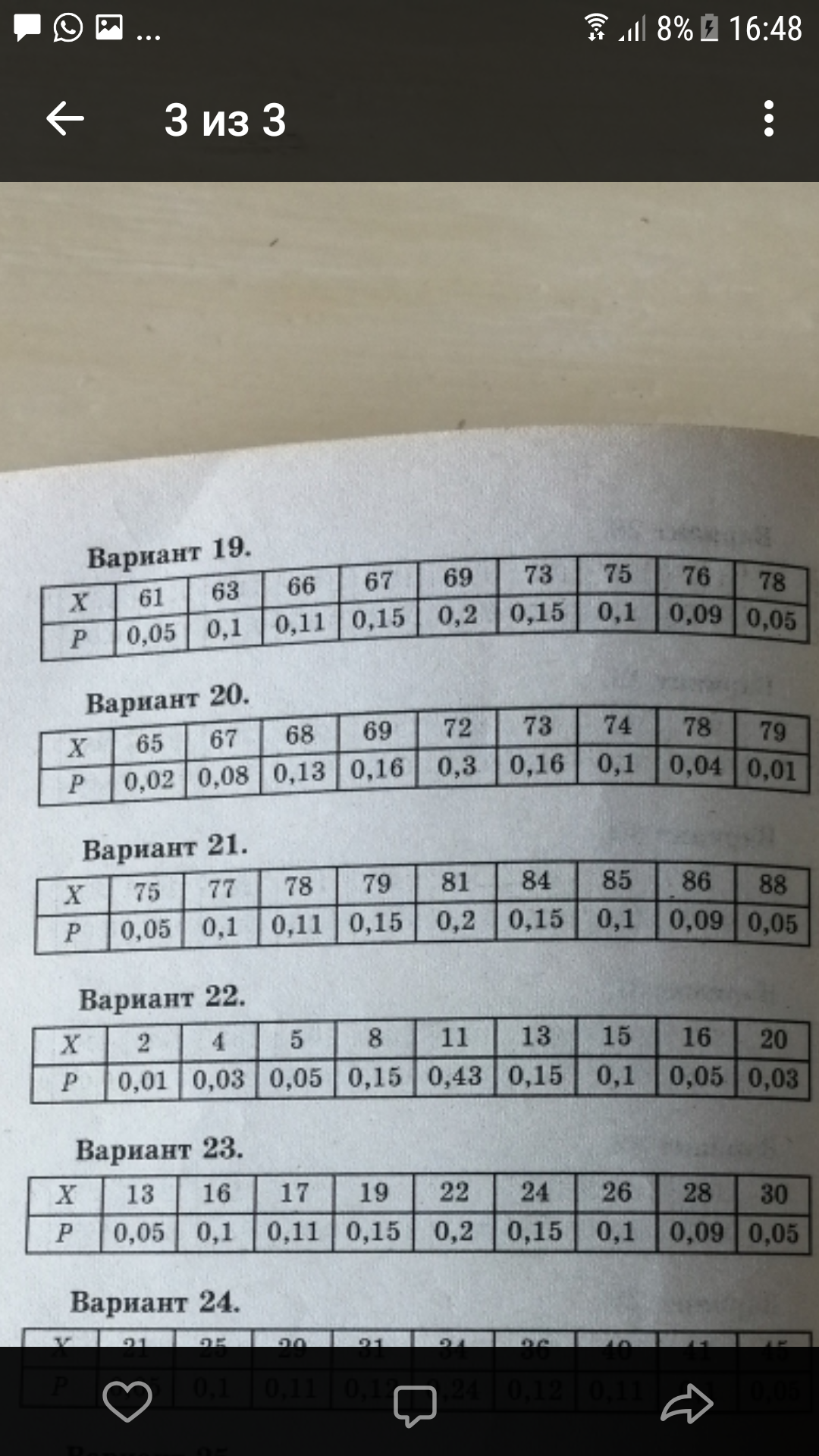
Х 25 27 30 32
P 0,2 0,4 0,3 0,1

Нужно решить 1 задачу по теории вероятностей.

Случайная величина х задана интегральной функцией распредения. Найти дифференциальную функцию распредения и числовые характеристики случайной величины х. Построить графики интегральной и дифференциальной функций распредения.

Непрерывная случайная величина Х имеет следующую плотность распределения:

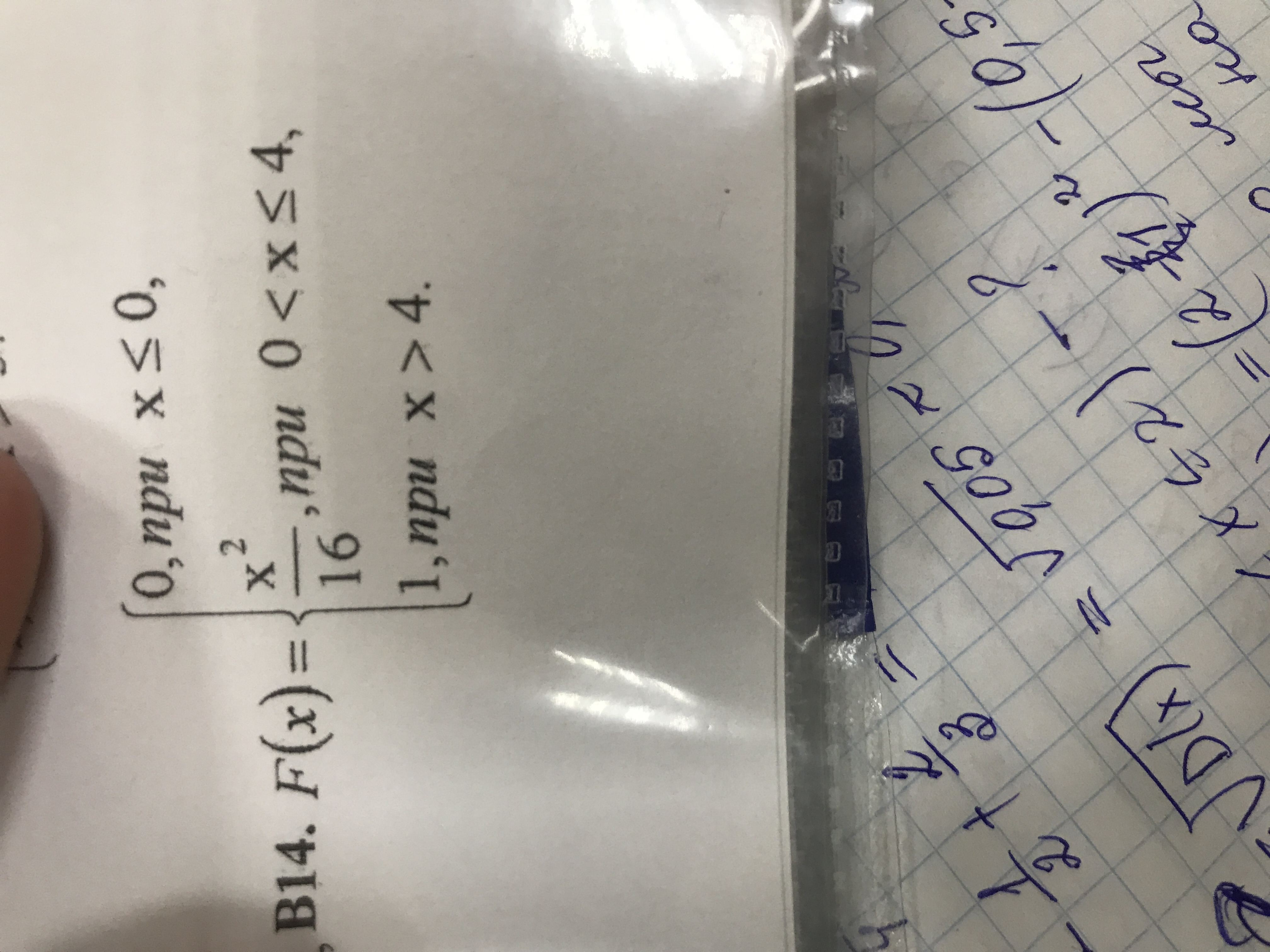
p(x) = { 0 при x ≤ 1, a/x³ при x > 1 }

Найти, округляя все ответы до сотых: 1. Коэффициент а 2 Р Вероятность попадания случайной величины Х] в интервал (2]3)| 0,19 З. Вероятность того, что при трех независимых испытаниях случайная величина Х ни разу не попадет в интервал (2, 3) 0,54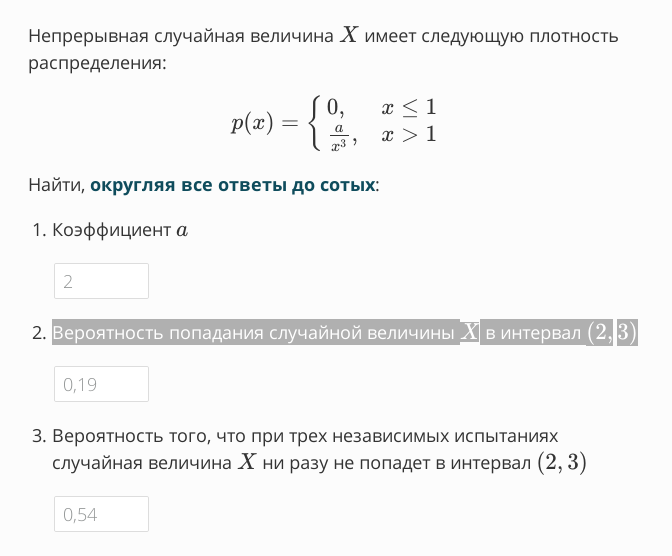

В партии из 12–ти деталей имеется десять стандартных. Наудачу отобраны три детали. Составить закон распределения числа стандартных деталей среди отобранных.

Ймовірність влучення у ціль першим пострілом дорівнює 0,8. З кожним наступним пострілом ймовірність зменшується на 0,1. Знайти закон розподілу і функцію розподілу числа влучень у ціль, якщо зроблено три постріли. Обчислити математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини.

Построить график функций f(x), F(X)

F(x) =
{ 0, при x ≤ 0,
{ x³ / 8, при 0 < x ≤ 2,
{ 1, при x > 2.

8. Вероятность попасть в самолет при выстреле из ружья равна 0.001. Произведено 3000 выстрелов. Составить закон распределения случайной вели¬чины – числа попаданий в самолет

Найти математическое ожидание и дисперсию непрерывной случайной величины Х, заданной функцией распределения

Независимые случайные величины Х, Z могут принимать только целые значения: Х : 1,2,3,4,5,6, 7 с вероятностью 1/7 , а Z только значения 7 и 14, при этом Р(Z = 7) = 3/5. Найдите вероятность того, что Х+Z = 9. Найти математическое ожидание М(Z).

Проводится n независимых испытаний , в каждом из которых A появляется с постоянной вероятностью p(0<p
1)Составить для числа появление событие A в этих испытаниях соответствующие распределения, найти M(x),D(x),b(x)
1)биноминальное распределение
2)Распределение Пуассона
1) n =3 p=0,85 2)n=100 p=0,01

в ящике находится 5 красных и 4 синих шара. из него последовательно вынимают шары до первого появления красного шара. построить закон распределения ДСВ Х – числа извлеченных шаров

7. Дана функция плотности распределения
[m]
\begin{align*}
0, &\; x < 2, \\
f(x) = A(x - 3)^{2}; &\; 2 \le x \le 4, \\
0, &\; x > 4.
\end{align*}
[/m]
Найти A и указать явный вид [m] f(x); M(x); D(x); F(x); P(x < 3); P(x \ge 3); P(2,5; 3,5). [/m]

8. Случайная величина X имеет нормальное распределение с математическим ожиданием a = 25. Вероятность попадания X в интервал (10; 15) равна 0,09. Найти вероятность того, что случайная величина X хотя бы один раз из четырех попадает в интервал (20; 35).

В урне 2 белых и 3 чёрных шара из урны последовательно вытаскивают по одному шару до тех пор пока не будет вытащен чёрный Х–число шаров в урне составить ряд распределения случайной величины построить график функции распределения найти мат ожидания дисперсию

Непрерывные случайные величины. Найти: А) Значение константы A Б) Математические ожидания случайных величин x и y В) Ковариацию случайных величин

Задача номер 10, выполнить ход решения и получить ответ

Задача 2.9. Зная функцию распределения случайной величины X:

[m]
F(x) =
\begin{cases}
0, & x < 0 \\
x - \frac{1}{4}x^2, & 0 \le x \le 2 \\
1, & x > 2
\end{cases}
[/m]

найти дифференциальную функцию [m]f(x)[/m] и построить ее график. Определить [m]P(0 \le x \le 1)[/m].

Задача 2.10. Случайная величина X распределена по закону, график которой имеет вид, изображенный на рисунке:

Найти A, функцию плотности f(x), математическое ожидание и среднее квадратичное отклонение.

2.11. Найти параметр С, математическое ожидание и дисперсию показательного распределения, заданного плотностью распределения

f(x) = C·e^–5x (x ≥ 0)

Найти вероятность того, что в результате испытания случайная величина Х попадет в интервал (0.1;0.2).

Задание 1. Непрерывная случайная величина задана функцией распределения F(x).
ННеобходимо найти: а) вероятность попадания случайной величины в интервал (с.В):
6) плотность распределения случайной величины /(:);

в) математическое ожидание м(х). дисперсию р(х) и среднее квадратическое
отклонение с(х). Построить графики функций F(x) H f(x).

Дана функция распределения непрерывной случайной величины F(х). Найти: параметр с; математическое ожидание; дисперсию; среднеквадратическое отклонение; — построить — график F(х); вероятность попадания случайной величины в промежуток X € [–p/3; 0]

Помогите срочно !!
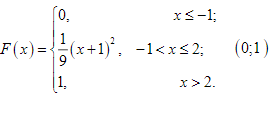
у меня еще день до сдачи задания ,спасибо!!!!!

Есть 3 урны. В первой урне 6 желтых и 4 синих шарика, во второй урне–7 желтых и 3 синих, а в третьей–2 желтых и 8 синих. Из каждой урны вынимают на удачу по одному шарику. Построить закон распределения случайной величины–появления числа синих шариков среди трех наугад взятых. Определить закон распределения F(x) и построить график функции.

29. Статистичними дослідженнями за рік встановлено,
що денний попит на товар має 4 різні варіанти.

[m]
\begin{array}{|c|c|c|c|c|}
\hline
X & 1 & 2 & 3 & 4 \\
\hline
P & 0,1 & 0,5 & 0,3 & 0,1 \\
\hline
\end{array}
[/m]

Знайти математичне сподівання та дисперсію попиту на товар.

Варіанти відповідей: а) 2,4; 0,64; б) 2,2; 0,64; в) 2,2; 5,4; г) 2,4; 5,4.

Ймовірність банкрутства кожного з двох банків є розв’язком системи рівнянь. Випадкова величина X — число банків, які зазнали банкрутства. Знайти математичне сподівання M(X) та дисперсію D(X) випадкової величини X.

32. { 2p₁ + 5p₂ = 2.2;
p₁ – 2p₂ = –0.7.

Товаровед проверяет изделия на стандартность, но
проверяет не более пяти изделий. Составить закон распределения числа проверенных изделий, если вероятность того, что изделие будет признано стандартным, равна 0,6. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение полученной случайной величины

1. В аптеку поступают препараты трех поставщиков. 15% препаратов поставляет первый поставщик ...

2. Из пяти гвоздик, среди которых три белые, наудачу выбирают две гвоздики. Составить закон распределения дискретной случайной величины X – числа выбранных белых гвоздик. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.

3. Нормальная непрерывная случайная величина X задана...

4. При измерении минутного объема сердца у случайно отобранных пациентов кардиологической клиники получены следующие результаты (в литрах): 4,2; 5,0; 4,0; 4,5; 4,2; 4,5. Требуется 1) построить дискретный ряд распределения выборки и полигон относительных частот; 2) найти основные числовые характеристики выборочной совокупности; 3) указать точечные оценки основных числовых характеристик генеральной совокупности; 4) с доверительной вероятностью у 0.99 найти доверительный интервал для истинного минутного объема сердца; 5) найти абсолютную и относительную погрешности измерения. Предполагается, что изучаемая величина распределена по нормальному закону.

ТЕСТ

1. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | –1 | 2 |
|–––|––––|–––|
| P | 0,3 | 0,7 |

Тогда математическое ожидание M(X) этой случайной величины равно ...
a) 1 . b) – 1,7. c) 1,1. d) 0,4.

2. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | –1 | 4 |
|–––|––––|–––|
| P | 0,4 | 0,6 |

Тогда математическое ожидание M(X) этой случайной величины равно ...
а) 2,1. b) 2. c) – 1. d) –2,7

3. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | –5 | 6 |
|–––|––––|–––|
| P | 0,5 | 0,5 |

Тогда математическое ожидание M(X) этой случайной величины равно ...
а) –0,5. b) 2. c) 1,5. d) –2,5.

2. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | –1 | 4 |
|:––––––:|:––:|:––:|
| P | 0,4|0,6|

Тогда математическое ожидание M(X) этой случайной величины равно …
a) 2,1. b) 2. c) –1. d) –2,7

4. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | –3 | 2 |
| P | 0,2 | 0,8 |

Тогда математическое ожидание M(X) этой случайной величины равно …
a) 1,0. b) –2.5. c) – 1. d) – 0,7

5. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | 8 | 10 |
| P | 0,3 | 0,7 |

Тогда математическое ожидание М(X) этой случайной величины равно …
a) 18. b) – 9,4. c) 9,4. d) 1.

6. Дискретная случайная величина X имеет закон распределения вероятностей:

| X | –2 | 3 |
| P | 0,4 | 0,6 |

Тогда математическое ожидание М(X) этой случайной величины равно …
a) 1. b) 2,9. c) 0,8. d) – 6.

Устройство состоит из 4 независимых работающих элементов. Все в одном испытании
вероятность отказа элементов
0,15. Отказ от работы на разовых испытаниях
сформулируйте правило распределения остальных элементов.

Задана плотность распределения непрерывной случайной величины Х. Sova видел вы уже решали такую задачку. Решение нашел, вот только график не могу построить, если можно то нужно график

Случайная величина Х задана функцией распределения

Вопрос № 8.

Непрерывная случайная величина Х имеет показательный закон распределения с параметром
λ = 4/5. Найти М(4Х + 3).

Вопрос №5.

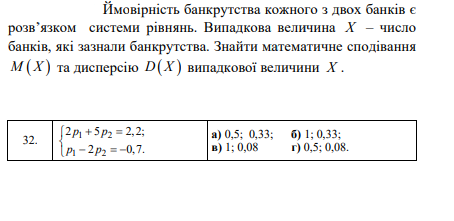
Дана функция распределения вероятностей непрерывной случайной величины [m] \xi [/m]:

[m]
F_{\xi}(x) =
\begin{cases}
0, & x \leq 0, \\
9x^2 & 0 < x \leq \frac{1}{3}, \\
1, & x > \frac{1}{3}.
\end{cases}
[/m]

Для случайной величины [m] \xi [/m] найдите значение выражения [m] 9 M(\xi) [/m], где [m] M(\xi) [/m] – это математическое ожидание этой случайной
величины.

Предположим, что цена на акции определенной компании является случайной величиной, распределенной по нормальному закону с математическим ожиданием 52 у.е. и уравнение квадратного отклонения 6 у.е. Определить вероятность того, что в случайно выбранный день цена за акцию была: а) свыше 55 у.е; б)53 у.е за акцию

3. Завод изготовляет валики, каждый из которых имеет дефект с вероятностью 0,07. валик проверяется одним контролером, обнаруживающим дефект с вероятностью 0,85. Кроме того, контролер может забраковать валик, не имеющий дефекта, с вероятностью 0,1. Найти вероятность того, что валик будет забракован.

4. В партии из 9 книг имеется 5 неправильно сброшюрованных книг. Наудачу отбирают 3 книги. Составить закон распределения случайной величины X—числа неправильно сброшюрованных книг среди отобранных. Найти математическое ожидание и дисперсию этой случайной величины.

Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 1.6 и 1. Какова вероятность того, при четырех испытаниях Х попадает хотя бы один раз в интервал (1.2)

pξ(x) = { 0, x < 0,              A · x · e^–x, x ≥ 0. } Найдите:  a. значение константы A;

Дана плотность распределения случайной величины икс, найти параметр а.

В урне a черных шаров и b белых. Из нее по схеме с возвращением вынимаются два шара. Случайная величина ξ равна количеству вынутых черных шаров. Найдите распределение этой случайной величины. Если в ответе значениям 0, 1 и 2 соответствуют вероятности p0, p1 и p2, то введите в систему выражение p0∗x+p1∗y+p2∗z. Задачу вроде бы решил.Однако, решение не принимается. Прошу содействия.
factorial(b)·factorial(a+ b –2)/(factorial(b–2)·factorial(a+b))·x+2·y·(factorial(a)·factorial(a)·factorial(a+b–2))/(factorial(a–1)·factorial(a+b)·factorial(a–1))+z·factorial(a)·factorial(a+b–2)/(factorial(a–2)·factorial(a+b))

У стрелка вероятность промаха равна 7/11. Боекомплект состоит из трёх патронов, стрельба продолжается до поражения цели или до исчерпания боекомплекта...

Задание на картинке

1. (6 б.) У стрелка вероятность промаха равна 4/9. Боекомплект состоит из трёх патронов, стрельба продолжается до поражения цели или до исчерпания боекомплекта. Закон распределения числа выстрелов (величины X) может быть задан таблицей:

2. (6 б.) У стрелка вероятность промаха равна 3/5. Боекомплект состоит из трёх патронов, стрельба продолжается до поражения цели или до исчерпания боекомплекта. Закон распределения числа выстрелов (величины X) может быть задан таблицей:

Устройство состоит из трёх независимо работающих элементов.Вероятность отказа каждого элемента в одном опыте равна 0.1. составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание дисперсию и средне квадратичное отклонение

Срочнооооооо помогите очень прошу
РЕШЕНИЕ+ГРАФИК

Решение+график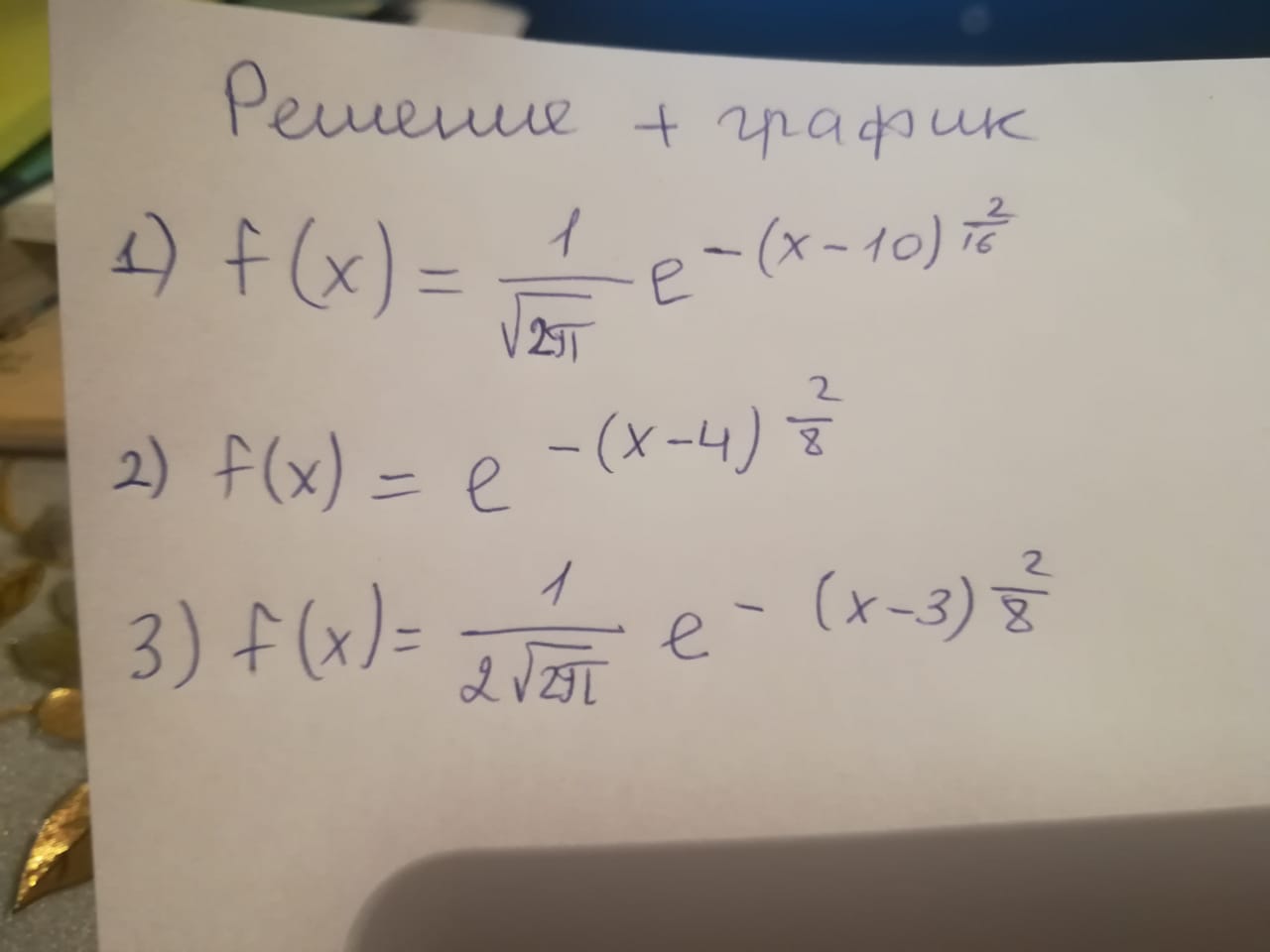
Помогите пожалуйста до утра срочноооооо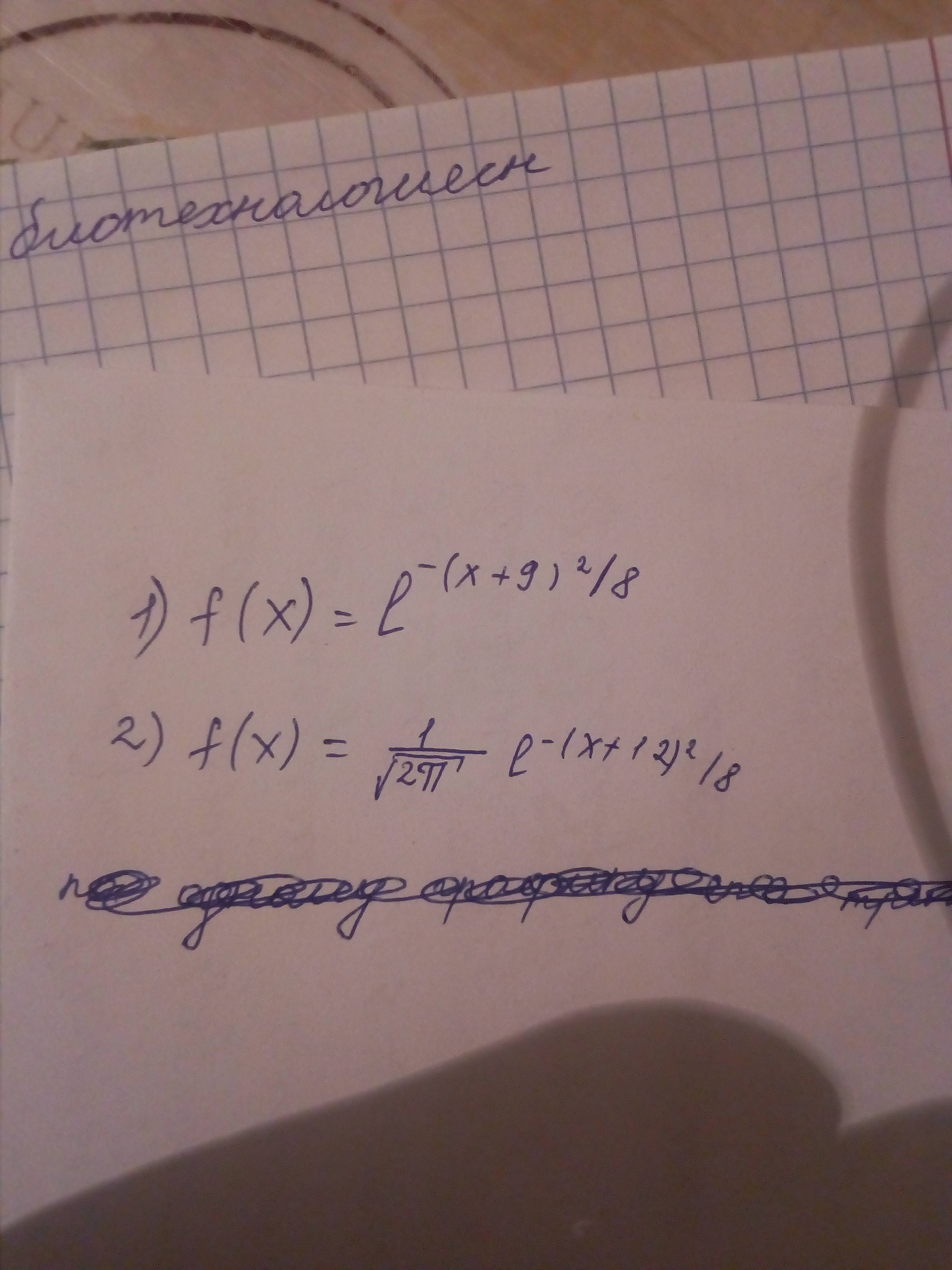

Найти математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной следующим законом распределения:

Валики, изготовляемые автоматом, считаются стандартными, если отклонение диаметра валика тт проектного размера не превышает 2мм.случайные отклонения диаметра валиков подчиняются нормальному закону со средним квадратическим отклонением 1.6 мм и математическим ожиданием, равным 100мм. Сколько процентов стандартных валиков изготовляет автомат?

Вариант 8.

X 67 68 71 74 76 78 81 84 88
P 0,05 0,1 0,11 0,15 0,17 0,15 0,12 0,1 0,05

Решите 7 вариант пожалуйста

Решите 20 вариант пожалуйста! Найти по закону распределения случайной величины