Задача 43378 3. Завод изготовляет валики, каждый из...
Условие
4. В партии из 9 книг имеется 5 неправильно сброшюрованных книг. Наудачу отбирают 3 книги. Составить закон распределения случайной величины X—числа неправильно сброшюрованных книг среди отобранных. Найти математическое ожидание и дисперсию этой случайной величины.
Решение
Вводим в рассмотрение гипотезы:
Н_(1)- деталь дефектная
p(H_(1))=0,07;
Н_(2)- - деталь не имеет дефекта
p(H_(2))=0,93
А- "деталь забракована"
p(A/H_(1))=0,85
p(A/H_(2))=0,1
p(A)=p(H_(1))*p(A/H_(1))+p(H_(1))*p(A/H_(1))=
=0,07*0,85+0,93*0,1= считаем
4.
5 книг - неправильно сброшюрованных
9-5=4 книги - правильно сброшюрованных
Из 9 книг выбирают 3
X- число неправильно сброшюрованных книг
Х может принимать значения
0;1;2;3
p_(0)=(C^(0)_(5)*C^(3)_(4))/С^(3)_(9)=
p_(1)=C^(1)_(5)*C^(2)_(4)/С^(3)_(9)=
p_(0)=C^(2)_(5)*C^(1)_(4)/С^(3)_(9)=
p_(0)=C^(3)_(5)*C^(0)_(4)/С^(3)_(9)=
Считаем вероятности.
С^(k)_(n)=n!/(k!*(n-k)!)
C^(3)_(9)=9!/(3!*(9-3)!)=7*8*9/3!=84
(C^(0)_(5)=1
C^(3)_(4))=4
p_(0)=(C^(0)_(5)*C^(3)_(4))/С^(3)_(9)=4/84
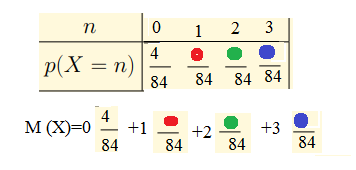
Составляем таблицу