Подкатегории (4)
Практика (48)
на каждом диске 5-ти буквенного кодового замка нанесено по 6 букв найти вероятность того что замок удастся открыть не более чем за пять попыток
Вероятность того, что наудачу взятая деталь не стандартная, равна 0,1. Найти вероятность того, что среди 5 взятых
наудачу деталей 4 будут стандартными.
С вероятностью 0,4 посланное сообщение принимается при одной передаче. Сколько надо сделать передач, чтобы с вероятностью не менее 0,9 она была принята хотя бы один раз?
В мастерскую для ремонта поступило 15 телевизоров. Известно, что 6 из
них нуждаются в общей регулировке. Мастер берет первые попавшиеся 5
телевизоров. Какова вероятность того, что 2 из них нуждаются в общей
регулировке?
Добрый вечер. Буду благодарен за помощь в решении этих задач. Хватит ответов на пять задач из восьми.


Во время тестирования по математике студент должен дать правильный ответ на 7 вопросов.
Вероятность того, что он ответит на один вопрос, в среднем равна 0,6. Найти
вероятность того, что студент сдаст тест, ответив на 4 вопроса.
Даю 50 балов

Вероятность выхода из строя за время Т одного конденсатора равна 0,2 Определить вероятность того, что за это время из 100 конденсаторов из строя выйдет не более 20 штук.
Стрелок стреляет по мишени, вероятность попадания при каждом выстреле равна 0,7. Найти
вероятность, что при пяти выстрелах он попадет более трех раз
Из семян данного растения обычно всходят 80%. Найти вероятность того, что прорастут 85 семян из 500 посаженных.
Монета брошена 40 раз. Найти вероятность того, что «герб» выпадет на 6 раз больше, чем «решка».
Требуется найти вероятность того,что в 5 независимых испытаниях событие появится более 3 раз, зная, что в каждом испытании вероятность появления события равна 0,7
На антобазе 12 автомашии. Вероятность выхода машины на линию одинакова для всех машин и равна 0.9. Найти вероятность того, что на линию выйдет в ближайший день 3 автомашины. Билет рассмотрен утвержден на заседании кафедры
В крупной партии деталей 20% бракованных. Для контроля отбирается пять деталей. Найти вероятность того, что ровно одна деталь окажется бракованной, хотя бы одна окажется бракованной. По каким формулам считать, чтобы получились такие значения 2101/3125≈0.673, 256/625≈0.410
1. Из 10 проданных за день холодильников 4 имеют скрытые дефекты. Найти вероятность того, что среди выбранных наудачу 5 холодильников будет: а) два холодильника без скрытых дефектов; б) не более одного холодильника со скрытым дефектом.
2. Клиент сотового оператора решил посетить офис связи и пополнить
111. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех? б) выиграть не менее двух партий из четырех или не менее трех партий из пяти? Ничьи
во внимание не принимаются.
№1 Среди 100 лоторейных билетов есть 20 выиграшных :
1. найдите вероятность того, что три наудачу выбранных билета окажутся выиграшными
2. найдите вероятность того, что среди двух наудачу выбранных билетов есть выигрышные
№2 Подбрасываются одновременно два игровых кубика. Найдите вероятность того, что одновременно выпадут числа:
1. две двойки
2. три и четыре
4.13(1). Всхожесть семян лимона составляет 80 %.
Найти вероятность того, что из девяти посеянных семян взойдут:
а) 7 семян; б) более семи.
В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное число денежных знаков, равна 0,0001. Найти вероятность того, что при проверке будет обнаружено три ошибочно укомплектованных пакета.
Электронная система состоит из 40 блоков, каждый из которых может отказать в течение года с вероятностью 0,05. Найти вероятность того, что откажет ровно 2 блока из 40.
Из N изделий М имеют скрытый дефект. Наугад выбрано n изделий. Найдите вероятности
следующих событий:
A –– среди выбранных m изделий имеют скрытый дефект;
B –– среди выбранных есть хотя бы одно изделие со скрытым дефектом;
C –– среди выбранных не более двух изделий со скрытым дефектом.
N=12 M=5 n=3 m=2
в колхозном саду посажено 7 саженцев вишни. Вероятность прижиться для каждого из саженцев одинакова и равно 0.9. Найти вероятность того, что приживется 5 саженцев. (ф-ла Бернулле)
В партии деталей 15% нестандартных. Найти вероятность того, что из 100 отобранных деталей нестандартными окажутся 15.
Вероятность попадания в цель при одном выстреле равна 0,25. Произве-
дено 6 выстрелов. Найти вероятность поражения цели, если для этого достаточ-
но хотя бы одного попадания.
пусть вероятность того, что покупателю потребуется обувь 41-го размера, равна 0,2. Найдите вероятность того, что равно 3 из 5 первых покупателей
потребуют обувь сорок первого размера
Вопрос № 3.
Вероятность попадания в мишень при одном выстреле равна 0.2. Определите вероятность того, что при 100 выстрелах мишень будет поражена от 8 до 20 раз.
Справка: ф(0)=0.3989; ф(1)=0,2420; Ф(0)=0; Ф(1)=0,3413; Ф(3)=0,4986,
где ф(х) - локальная, а Ф(х) - интегральная функция Лапласа.
Предположим, что цена на акции определенной компании является случайной величиной, распределенной по нормальному закону с математическим ожиданием 52 у.е. и уравнение квадратного отклонения 6 у.е. Определить вероятность того, что в случайно выбранный день цена за акцию была: а) свыше 55 у.е; б)53 у.е за акцию
Среди 100 билетов денежно-вещевой лотереи 10 выигрышных. Сколько лотерейных билетов нужно купить, чтобы с вероятностью не меньшей 0,986, быть уверенным в выигрыше хотя бы по одному билету?
Вероятность появления события А в опыте равна 0,2. Опыт повторили независимым образом 400 раз. Какова вероятность того, что при этом событие А произойдет: а) 80 раз; б) не менее 70 и не более 90 раз?
Цена некоторой ценной бумаги имеет нормальное распределение с математическим ожиданием 120 ден.ед. и средним квадратическим отклонением 20 ден.ед. Найти: 1) вероятность того, что цена акции в день покупки будет не выше 130 ден.ед; 2) отклонится от математического ожидания по абсолютной величине менее, чем на 10 ден.ед.;
Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 1.6 и 1. Какова вероятность того, при четырех испытаниях Х попадает хотя бы один раз в интервал (1.2)
1. ОТК проверяет изделия на стандартность. Вероятность, что изделие ока- жется стандартным, равна 0,95. Найти вероятность, что из трех изделий хотя бы одно окажется нестандартным.
2. Есть два ящика. Первый ящик содержит 7 деталей (4 стандартных и 3 бракованных), второй — 9 деталей (5 стандартных и 4 бракованных). Под- бросавется игральный кубик, и если выпадает четное число очков, то извлекают 2 детали из первого ящика, а если выпадает нечетное число очков, то извлекают 2 детали из второго ящика. Найти вероятность, что обе извлеченные детали стандартные.
В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно три раза.
2. Произведено 900 независимых испытаний, в каждом из которых вероятность наступления события А равна 0,25. Найти: а) наивероятнейшее число наступлений события А - К0; б) вероятность того, что событие А наступит К0 раз.
8. Среднее число вызовов, поступающих на АТС в 1 мин, равно 5. Найти вероятность того, что за 2 мин поступит: а) два вызова; б) менее двух вызовов; в) не менее двух вызовов.
1. Сборник содержит 600 задач с ответами. В каждом ответе может быть ошибка с вероятностью 0,001. Какова вероятность того, что: а) ответы в 5 задачах даны с ошибками; б) хотя бы в трех ответах есть ошибки?
3. В партии 6 деталей. Вероятность отклонения размера каждой детали от стандарта равна 0,23. Найти вероятность того, что в данной партии отклонение размера будет менее, чем у трех деталей.
4. Найти вероятность того, что при проведении 600 испытаний событие А появится не менее 400 раз, если вероятность появления события А в каждом испытании равна 0,65. Какова вероятность, что событие А появится ровно 410 раз?
Страховая компания проводит страхование n однотипных объектов. Вероятность наступления
страхового случая для каждого из объектов (независимо от других) за время t равна p. Найдите
вероятность того, что за время t страховой случай:
1) не наступит;
2) наступит не менее двух раз.
n=10, p=0,3
178. Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно четыре бракованных.
вероятность выхода из строя за время t одного конденсатора равна 0,2
найдите вероятность того, что за время t из 100 независимо работающих конденсаторов из строя выйдут от 14 до 26
Завод отправил на базу 5000 изделий.Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что:
а) на базу придут ровно 3 негодных изделия:
б) что вся партия будет целой.
5. Найти среднее число опечаток на странице рукописи, если вероятность того, что страница рукописи содержит хотя бы одну опечатку, равна 0,95. Предполагается, что число опечаток распределено по закону Пуассона.
Книга издана тиражом 10 тыс. экземпляров. Вероятность того, что книга сброшюрована неправильно, равна 0,0002. Найти вероятность того, что тираж содержит бракованных книг а) равно 5; б) от 3 до 5.
Здравствуйте, помогите, пожалуйста, решить задачу по схеме Бернули. Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останется не менее двух.
В среднем 10% изготавливаемых деталей являются иестандартными. Найти вероятность того, что
нестандартных деталей из 100 отобранных для проверки будет 7 Уштук: от 8 1011
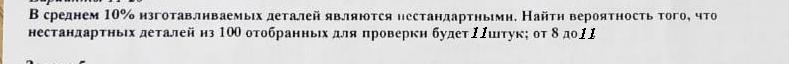
1. В партии содержится шесть деталей. Считая вероятность появления стандартной и нестандартной детали одинаковыми, определить вероятность того, что в указанной партии содержится три стандартных детали; не менее пяти стандартных деталей.
3. Вероятность того, что на странице книги могут оказаться опечатки,
равна 0,0025. Проверяемая книга содержит 800 страниц. Какова вероятность
того, что с опечатками окажется 5 страниц?