Задача 43241 Случайная величина X распределена...

nika11111

2020-01-06 12:29:27

Случайная величина X распределена нормально. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 1.6 и 1. Какова вероятность того, при четырех испытаниях Х попадает хотя бы один раз в интервал (1.2)

sova

2020-01-07 12:27:21

a=1,6
σ =1

α =1
β =2

[m]p( \alpha <X<\beta )=\Phi (\frac{ \beta -a}{ \sigma })-\Phi (\frac{ \alpha -a}{\sigma })[/m]

[m]\frac{ \beta -a}{ \sigma }=\frac{2-1,6}{1}=0,4[/m]

[m]\frac{ \alpha -a}{ \sigma }=\frac{1-1,6}{1}=-0,6[/m]

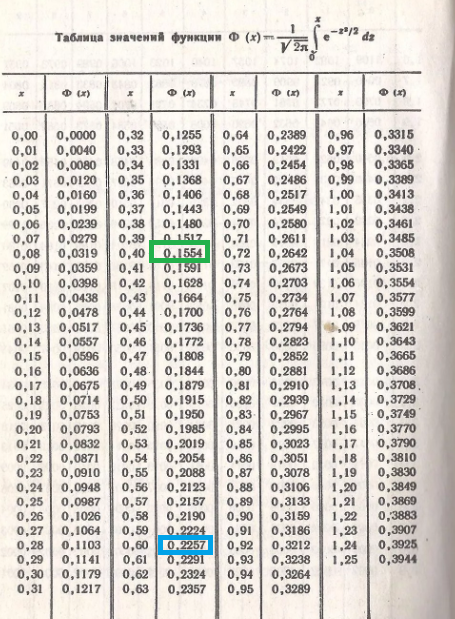
[m]\Phi (\frac{ \beta -a}{ \sigma })=\Phi(0,4) ≈0,1554 [/m]

[m]\Phi (\frac{ \alpha -a}{ \sigma })=\Phi(-0,6)=-\Phi(0,6) ≈ -0,2257[/m]

cм. таблицу значений функции Лапласа

[m]p( 1 <X<2 )=0,1554-(-0,2257)=0,1554+0,2257=0,3811[/m]

- вероятность попадания случайной величины, распределенной по нормальному закону с m=1,6 и σ =1 в интервал (1;2)

Введем в рассмотрение событие А

A-"при четырех испытаниях Х попадает хотя бы один раз в интервал (1.2)"

Тогда
vector{A}-"при четырех испытаниях Х не попадает ни разу в интервал (1;2)"

p(vector{A})=P_(4)(0)

По формуле Бернулли:

P_(4)(0)=C^(0)_(4)p^(0)q^4

p=0,3811
q=1-p=1-0,3811=0,6189


p(vector{A})=P_(4)(0)=4*(0,6189)^4

p(A)=1-p(vector{A})=1-4*(0,6189)^4 считаете и получаете ответ