Статистика

Анализируя результаты ОГЭ по математике своих учеников, учитель получил таблицу частот. Изучи данные из таблицы и, заменив каждый интервал на его середину, определи, какое количество баллов в среднем получили ученики.

Заполните последний столбец таблицы (с точностью до тысячных)

1. Дан набор случайных названных трезнячных чисел: 367, 417, 521, 148, 317, 526, 667, 957, 584, 124, 649. Составьте таблицу распределения по частотам М значений случайной величины Х — цифр, встречающихся в наборе.

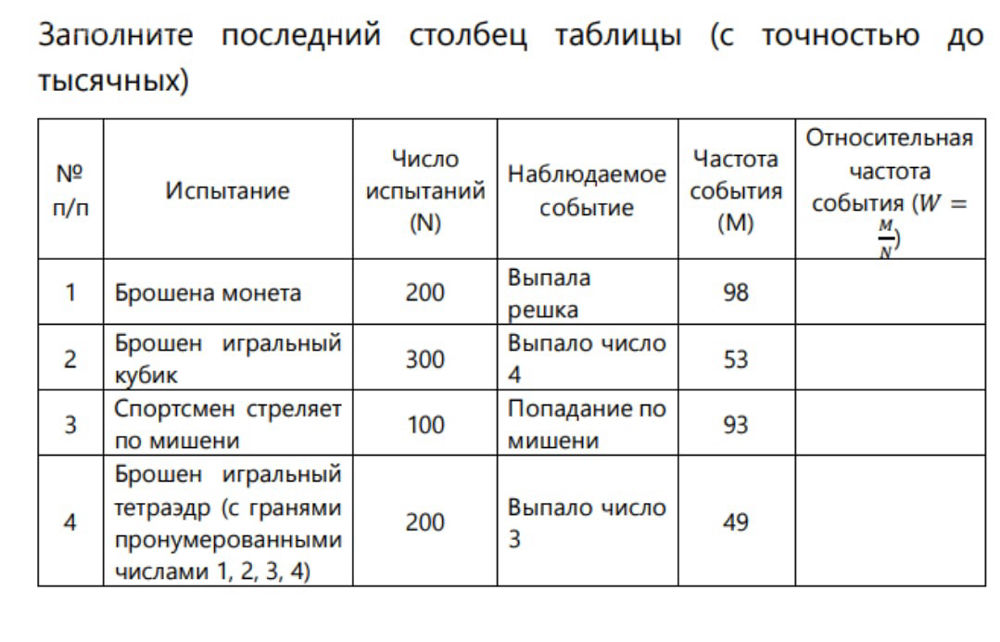
2. Постройте полигон частот и полигон относительных частот значений случайной величины Х, распределение которой представлено в таблице:

X | 4 | 5 | 6 | 7 | 8 | 9 | 10
M | 2 | 5 | 6 | 7 | 5 | 4 | 6

3. Найдите размах, моду, медиану и среднее выборки:
1, 14, -4, -5, 15, 0, 12, 0, -7.

Построить гистограмму относительных частот по данному распределению:

Найти выборочную дисперсию по данному распределению выборки объема n=50

Задание 2
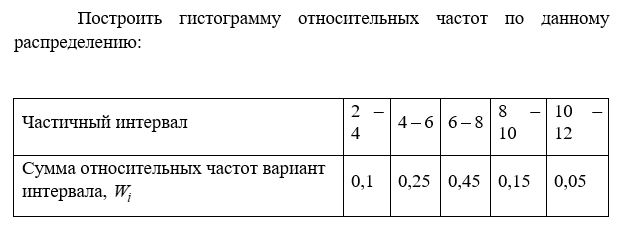
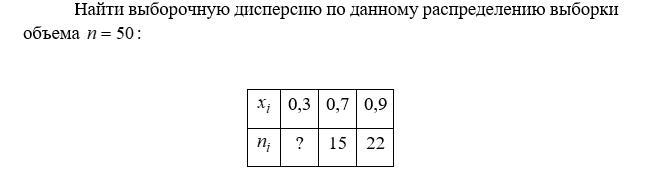
Дано статистическое распределение выборки:

| xi | 18,4 | 18,6 | 19,3 | 19,6 |
| n | 5 | 10 | 20 | 15 |

Определить среднее, моду, медиану, дисперсию и среднее квадратическое отклонение.

Задание 2

Дано статистическое распределение выборки:

| xi | 18,4 | 18,6 | 19,3 | 19,6 |
|----|------|------|------|------|
| ni | 5 | 10 | 20 | 15 |

Определить среднее, моду, медиану, дисперсию и среднее квадратическое отклонение.

449) Построить гистограмму относительных частот по данному распределению выборки:

Указание. Найти сначала относительные частоты, соответствующие
плотности относительной частоты для каждого интервала.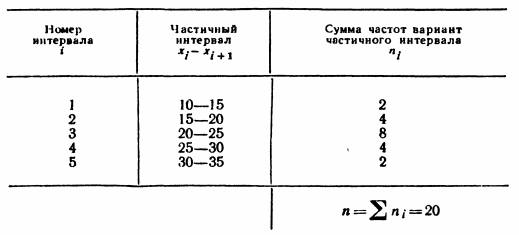

1. В аптеку поступают препараты трех поставщиков. 15% препаратов поставляет первый поставщик ...

2. Из пяти гвоздик, среди которых три белые, наудачу выбирают две гвоздики. Составить закон распределения дискретной случайной величины X - числа выбранных белых гвоздик. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины X.

3. Нормальная непрерывная случайная величина X задана...

4. При измерении минутного объема сердца у случайно отобранных пациентов кардиологической клиники получены следующие результаты (в литрах): 4,2; 5,0; 4,0; 4,5; 4,2; 4,5. Требуется 1) построить дискретный ряд распределения выборки и полигон относительных частот; 2) найти основные числовые характеристики выборочной совокупности; 3) указать точечные оценки основных числовых характеристик генеральной совокупности; 4) с доверительной вероятностью у 0.99 найти доверительный интервал для истинного минутного объема сердца; 5) найти абсолютную и относительную погрешности измерения. Предполагается, что изучаемая величина распределена по нормальному закону.

2. Построить полигоны частот и относительных частот распределения

10. Найти минимальный объем выборки, при котором с надежностью 0,95 точность оценки математического ожидания нормально распределенного признака по выборочной средней будет равна 0,2, если среднее квадратическое отклонение равно 2.

Дано статистическое распределение выборки:

xᵢ | 18,4 | 18,6 | 19,3 | 19,6
nᵢ | 5 | 10 | 20 | 15

Определить среднее, моду, медиану, дисперсию и среднее квадратическое отклонение.