Числовые характеристикики

Плотность вероятности непрерывной СВ X задана функцией f(x) . Найдите:
1) параметр С ;
2) интегральную функцию F[X];
3) постройте графики дифференциальной и интегральной функций;
4) определите P(a<x<b) дважды, используя дифференциальную функцию и интегральную функцию. Результат проиллюстрируйте на графиках.
5) числовые характеристики M[X] и D[Y] .

В 1 ЗАДАНИИ НАЙТИ ТОЛЬКО p(1<X<2)
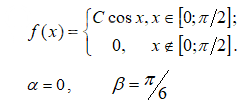
И 2 задание
Помогите пожвлуйста

Х задана плотностью распределения

system{ c*(1/x^4), x >= 2; 0, x < 2 }

Найти: а) константу с; 6) Числовые характеристики: математическое ожидание, дисперсию и среднее квадра t в) вероятность попадания случайной величины Х в интервал (2; 4).

306. Задана функция плотности вероятности непрерывной случайной величины Х ... Найдите числовые характеристики М(Х), D0 и ....

307. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины Х, заданной по показательному закону с функций плотности

Случайная величина Х распределена равномерно на отрезке [а; b ]. 1. Составить функцию распределения F(х) и функцию плотности f(х), построить их графики. 2. Вычислить математическое ожидание МХ и дисперсию DХ. 3. Вычислить вероятность попадания случайной величины Х в отрезок [с;d] . 4. Оценить вероятность неравенства |Х — МХ| > £ при помощи неравенства Чебышева. Вычислить эту вероятность непосредственно. а=-6, b=1,5 c=-8,5 d=0,3, £=0,3.

Случайная величина
X – годовой доход наугад взятого лица, облагаемого
налогом. Ее плотность вероятности имеет вид:
f(x)= {0, при x≤b
{
{a*x^(-1-n), при x>b
b=4 n=2,5
Требуется найти: а) значение параметра a;
б) функцию распределения F(x) случайной величины X;
в) математическое ожидание, дисперсию и среднее квадратичное отклонение;
г) размер годового дохода, не ниже которого с вероятностью 0,6 окажется годовой доход случайно выбранного налогоплательщика:
д) построить графики функций F(x), f (x).