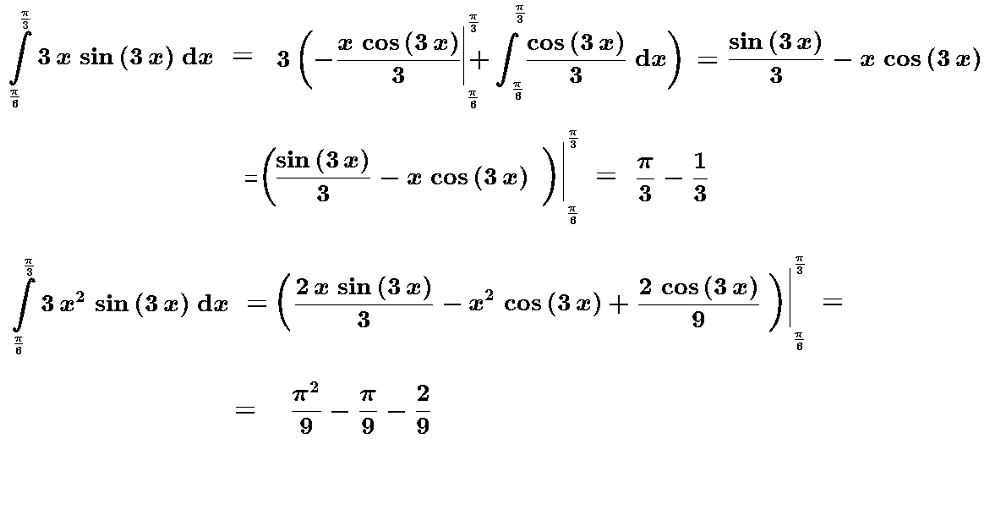Задача 68766 306. Задана функция плотности...
Условие
307. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение непрерывной случайной величины Х, заданной по показательному закону с функций плотности 
Решение
По определению:
[m]M(X)=∫ ^{∞ }_{- ∞ }x\cdot f(x)dx[/m]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{\frac{π}{6}}_{\frac{π}{3}}3xsin3xdx=...=\frac{π}{3}-\frac{1}{3}[/m]
Интегрирование по частям( см скрин)
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
Считаем
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X^2)=∫ ^{\frac{π}{6}}_{\frac{π}{3}}3x^2sin3xdx=...=\frac{π^2}{9}-\frac{π}{9}-\frac{2}{9}[/m]
Интегрирование по частям ( см скрин)
Тогда
[red]D(X)=\frac{π^2}{9}-\frac{π}{9}-\frac{2}{9}-(\frac{π}{3}-\frac{1}{3})^2=\frac{π}{9}-\frac{3}{9}[/red]
По формуле:
[m]σ(X)=\sqrt{ D(X)}=\sqrt{\frac{π}{9}-\frac{3}{9}}[/m]
307.
λ =10
M(X)=1/10
D(X)=1/100
σ (X)=sqrt(D(X))=1/10