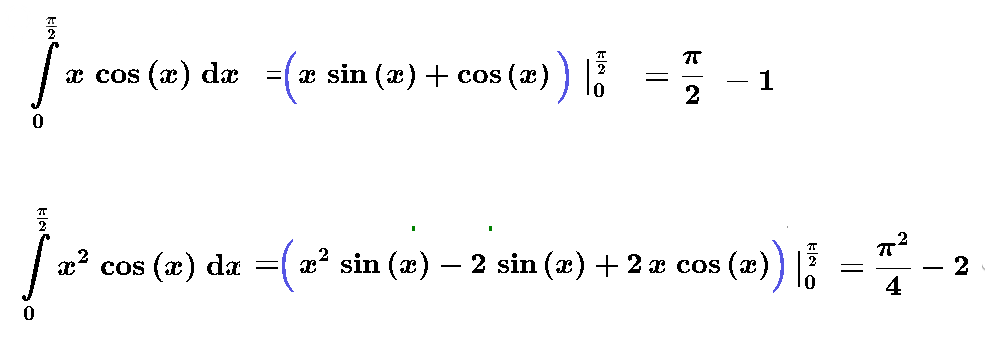Задача 77594 Плотность вероятности непрерывной СВ X...
Условие
1) параметр С ;
2) интегральную функцию F[X];
3) постройте графики дифференциальной и интегральной функций;
4) определите P(a<x<b) дважды, используя дифференциальную функцию и интегральную функцию. Результат проиллюстрируйте на графиках.
5) числовые характеристики M[X] и D[Y] .

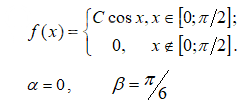
Решение
По свойству плотности:
∫ ^(∞ )_(- ∞ )f(x)dx=1
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний интегралы равны 0, так как функция равна 0):
∫^(π/2) _(0)(C*cosx)dx=C*sinx}|_(0)^(π/2)=C*(sin(π/2)-sin0)=C
[b]C=1[/b]
б)
[red]M(X)[/red]=∫ ^(∞ )_(- ∞ )x*f(x)dx=
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
= ∫ ^(π/2)_(0)(x*(cos))dx=... ( cм. скрин) =(π/2)-1
cчитаем по частям
u=x
dv=cosxdx
...
в)
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
Считаем
[red]M(X^2)[/red]=∫ ^(+ ∞ )_(- ∞ )x^2*f(x)dx= ∫^(π/2)_(0)(x^2*(cosx))dx=... ( cм. скрин) =(π^2/4)-2
cчитаем по частям два раза
u=x^2
dv=cosxdx
...
... ( cм. скрин) =(π^2/4)-2-((π/2)-1)^2=π-1
г)
[red]σ (Х)=sqrt(D(X))=sqrt(π-1)[/red]
д)
По формуле:
P( α ≤ x ≤ β )=F( β )-F( α )
P( 0 ≤ x ≤π/6 )=F(π/6 )-F(0 )=sin(π/6)-sin0=1/2
Находим функцию распределения.
По определению:
[blue][m]F(x)= ∫ _{- ∞ }^{x} f(x)dx[/m][/blue]
Поэтому:
при x ≤ 0
f(x)=0
и
F(x)= 0
При 0 < x ≤ π/2
[m]F(x)= ∫ _{0 }^{x}cosx dx=sinx[/m]
При x >π/2
F(x)=1
[m]F(x)=\left\{\begin{matrix} 0 & , x\leq 0 & \\sinx &,0 < x ≤ π/2& \\ 1& & ,x > π/2 \end{matrix}\right.[/m]