Задача 33634 ...
Условие
предмет не задан
955
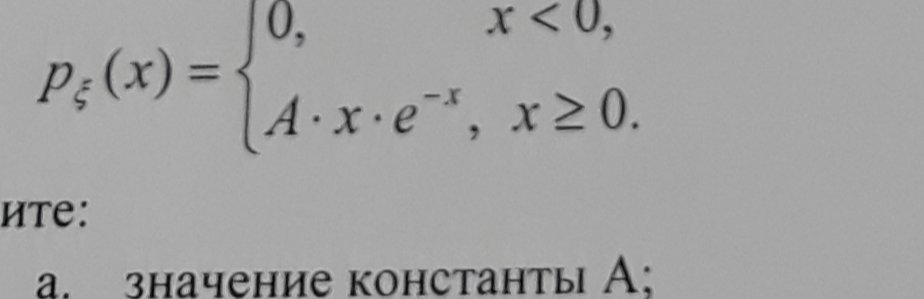
Решение
★
∫ ^(+ ∞ )_(- ∞ )p_(ξ)(x)dx=1
Считаем интеграл от данной функции.
Так как функция задана двумя выражениями рассматриваем интеграл как сумму интегралов:
∫^(+ ∞)_(- ∞ )p_(ξ)(x)dx=
=∫^(0)_(- ∞ )[b]0[/b](x)dx+∫^(+ ∞)_(0)[b]Axe^(-x)[/b]dx =
второй интеграл считаем по частям( константу А выносим за знак интеграла):
u=x
dv=e^(-x)dx
du=dx
v=-e^(-x)
=0 + A*(x*(-e^(-x))|(+ ∞)_(0) - ∫(+ ∞)_(0)(-e^(-x))dx=
=A*( 0 - e^(-x)|^(+ ∞)_(0)= A*(0- [b](0-1)[/b])=A
A=1
x*(-e^(-x))|(+ ∞)_(0)= lim_(x→+∞)(-x)/(e^(x)) - 0*e^(-0)=
предел по правилу Лопиталя равен 0
e^(-x))|(+ ∞)_(0)= lim_(x→+∞)1/(e^(x)) - e^(-0)=[b]0-1[/b]