Задача 61362 Нужно решить 1 задачу по теории...
Условие

Решение
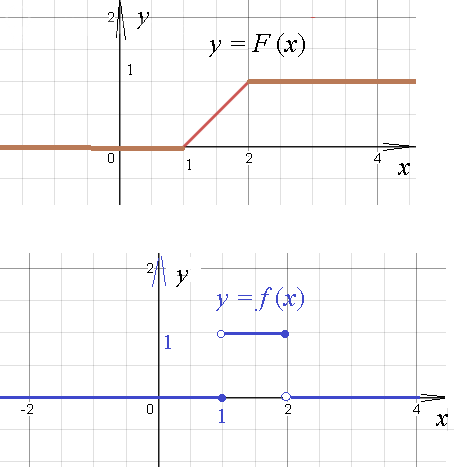
[m]f(x)=\left\{\begin{matrix}
0,если x ≤ 1\\1, если 1<x≤2 \\0, если x > 2\end{matrix}\right.[/m]
По определению:
[m]M(X)=∫ ^{∞ }_{- ∞ }x\cdot f(x)dx[/m]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{1}_{2}x\cdot 1dx=(\frac{x^2}{2})|^{1}_{2}=\frac{2^2}{2}-\frac{1^2}{2}=\frac{3}{2}[/m]
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
Считаем
[m]M(X^2)=∫ ^{∞ }_{- ∞ }x^2\cdot f(x)dx[/m]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{1}_{2}x^2dx=(\frac{x^3}{3})|^{1}_{2}=\frac{2^3}{3}-\frac{1^3}{3}=\frac{7}{3}[/m]
Тогда
[red][m]D(X)=M(X^2)-(M(X))^2=\frac{7}{3}-(\frac{3}{2})^2=\frac{1}{12}[/m][/red]
По формуле:
[m]P( α ≤ x ≤ β )=F( β )-F( α )[/m]
получаем:
[m]P( A)=P(-2 ≤ x ≤1 )=F(1 )-F(0)=0-0=0[/m]