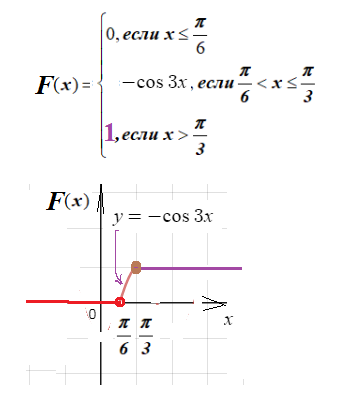Задача 47156 Задана плотность распределения...

prioraa844

2020-04-15 10:18:28

Задана плотность распределения непрерывной случайной величины Х. Sova видел вы уже решали такую задачку. Решение нашел, вот только график не могу построить, если можно то нужно график

sova

2020-04-15 11:18:32

★

Это график y=3sin3x
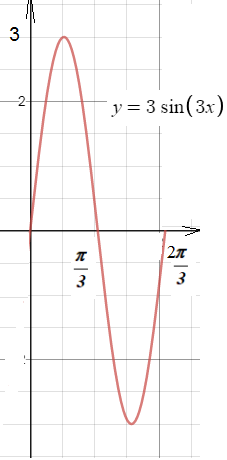
Амплитуда в три раза больше, т.е если обычный синус находится в полосе от -1 до1, то этот в полосе от -3 до 3

Период обычного синуса T=2π
Это означает, что полная волна синуса расположена на отрезке 2π

Период функции y=sin3x в три раза меньше, т.е равен (2π/3)

На рисунке, та часть синуса, которая выше оси оси Ох расположена на отрезке [0; π/3]

А обычный синус на отрезке [0; π]

Теперь Ваш вопрос, взять часть этого графика на отрезке [π/6;π/3]

До точки х=π/6 - прямая y=0 ( сама ось Ох), после точки x=π/3 - прямая y=0


По определению:

[r]F(x)= ∫ ^(x)_(- ∞ )f(x)dx[/r]

[b]При x ≤ π/6[/b]

F(x)= ∫ ^(x)_(- ∞ )[b]0[/b]dx=0

При [red] π/6 [/red]< x ≤ π/3

F(x)= ∫ ^(x)_([red]π/6[/red] )[b]3sin3x[/b]dx=(-cos3x)|^(x)_(π/6)=

=-cos3x+cos(3*π/6)=-cos3x+cos(π/2)=-cos3x+0=-cos3x

[green]При x > π/3[/green]

F(x)= ∫ ^(π/3)_(π/6)3sin3x=(-cos3x)|^(π/3)_(π/6)=-cos(3*π/3)+cos(3*π/6)=

=-cosπ+0=-(-1)=1