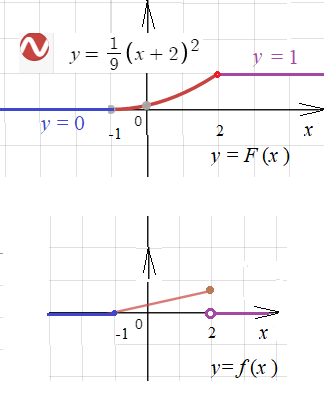Задача 54931 Задание 1. Непрерывная случайная...
Условие
ННеобходимо найти: а) вероятность попадания случайной величины в интервал (с.В):
6) плотность распределения случайной величины /(:);
в) математическое ожидание м(х). дисперсию р(х) и среднее квадратическое
отклонение с(х). Построить графики функций F(x) H f(x).

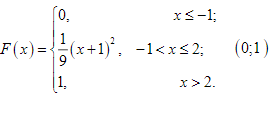
Решение
По формуле:
[m]P( α ≤ x ≤ β )=F( β )-F( α )[/m].
По условию дан [m] (0;1)[/m]:
[m] α =0[/m] и [m] β =1[/m]
[m]F(x)=\frac{1}{9}(x+1)^2[/m], поэтому
[m]P( 0 ≤ x ≤ 1 )=F( 1 )-F( 0 )=\frac{1}{9}(1+1)^2-\frac{1}{9}(0+1)^2=\frac{1}{9}\cdot (2^2-1)=\frac{3}{9}=\frac{1}{3}.[/m]
б)
Находим плотность по определению:
[m]f(x)=F `(x)[/m].
[m]f(x)=\left\{\begin{matrix}
0, если ...x ≤ -1\\\frac{2}{9}(x+1), если ...-1 < x ≤2 \\0, если ... x > 2\end{matrix}\right.[/m]
в)
По определению:
[red][m]M(X)=∫ ^{∞}_{- ∞}x\cdot f(x)dx[/m][/red]
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
[m]M(X)= ∫ ^{2}_{-1}(x\cdot \frac{2}{9}(x+1))dx=[/m]
считаем определённый интеграл
...
Дисперсию считаем по формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red] (#)
Находим по формуле:
[red][m]M(X^2)=∫ ^(+ ∞ )_(- ∞ )x^2\cdot f(x)dx[/m][/red]
Для данной задачи это:
[m]M(X^2)=∫ ^{2}_{-1}(x^2\cdot \frac{2}{9}(x+1))dx=[/m]
считаем определённый интеграл
подставляем в формулу (#) этого пункта
...
Средне квадратичное отклонение:
[red][m]σ (Х)=\sqrt{D(X)}[/m][/red]
...