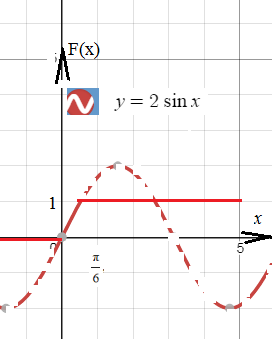
Задача 46507 Случайная величина Х задана функцией...
Условие

математика ВУЗ
1790
Решение
★
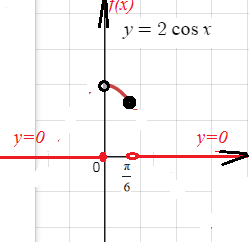
Находим плотность
f(x)=F `(x)
f(x)=
{0, x ≤ 0
{2cosx, если 0 < x ≤π/6
{ 0, x >π/6
б)
[red]M(X)[/red]=∫ ^(∞ )_(- ∞ )x*f(x)dx=
Так как функция задана на трех промежутках, то интеграл равен сумме интегралов по трем промежуткам (первый и последний равны 0, так как функция равна 0):
= ∫ ^(π/6)_(0)(x*(2cosx))dx=
cчитаем по частям
...
в)
По формуле:
[red]D(X)=M(X^2)-(M(X))^2[/red]
Считаем
[red]M(X^2)[/red]=∫ ^(+ ∞ )_(- ∞ )x^2*f(x)dx= ∫ ^(π/6)_(0)(x^2*(2cosx))dx=
cчитаем по частям два раза
...
г)
[red]σ (Х)=sqrt(D(X))[/red]
д)
По формуле:
P( α ≤ x ≤ β )=F( β )-F( α )
P( 0 ≤ x ≤ π/6 )=F( π/6 )-F( 0 )=2sin(π/6)=1