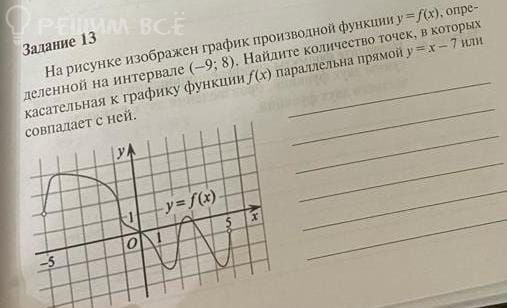Уравнение касательной, уравнение нормали, угловой коэффициент касательной

¢ Задание 13 на рисунке мзображен. график: производной ey = f(3), OnPE" деленной В8. интервале (–9; ®– ‘Найдите. количество, ‘дочек, BXOTOPE касательная & графику. sk 1) ‘параллельн® прямой у— ТМ ъ:пш\н:\цет сней. / – 18 '–"' / = аа & Illll= / i e 1 llI»l AT – "ШБ"ПП. т RN T U O g НЕОа Н e

Через начало координат провести прямую, отстоящую от точки (2, −3) на расстоянии 9/
√
17

Варіатн 1

Составить уравнение касательной и нормали к кривой в указанной точке (ЗАДАНИЕ 3)

Составить уравнения касательной и нормали к кривой:
1) у=х²— Зх + 4 в точке с абсциссой x=1;
9) у=4—х² в точке с абсциссой х =—1;
3) у= х³ + 2х — 1 в точке с абсциссой х =0;
4) y=.. в точке с абсциссой x=3.

Найти тангенс угла наклона касательной к графику функции f(x)=x³–3x²+13 в точке с абсциссой x0=3

Найти тангенс угла наклона касательной к графику функции f(x)=x³–3x²+2x+13 в точке с абсциссой x0=3

написать уравнение касательной к графику функции f (x) x2–3x+2 в точке с абсциссой x0= 0

Очень прошу о помощи!!! решить три задания. 1–2) составить уравнение касательной к графику функции в точке х0. 3 )исследовать функцию на монотонность и экстремумы.
очень–очень нужны правильные ответы. напрямую зависит годовая оценка????

Найти угловой коэффициэнт касательной графику функции f(X)=3^x; x0=1

Вычислите угол, под которым график функции [m]f(x)=x^3-1[/m] пересекает ось абсцисс.

Вычисли, в какой точке графика функции y=f(x) касательная параллельна заданной прямой:

y=4+5x, f(x)=x33−3x2+14x−3.

Ответ (при необходимости округли с точностью до десятых):

касательная параллельна заданной прямой в точке с координатами???

Составьте уравнение касательной к параболе x²=4y в точке A(1,–2)

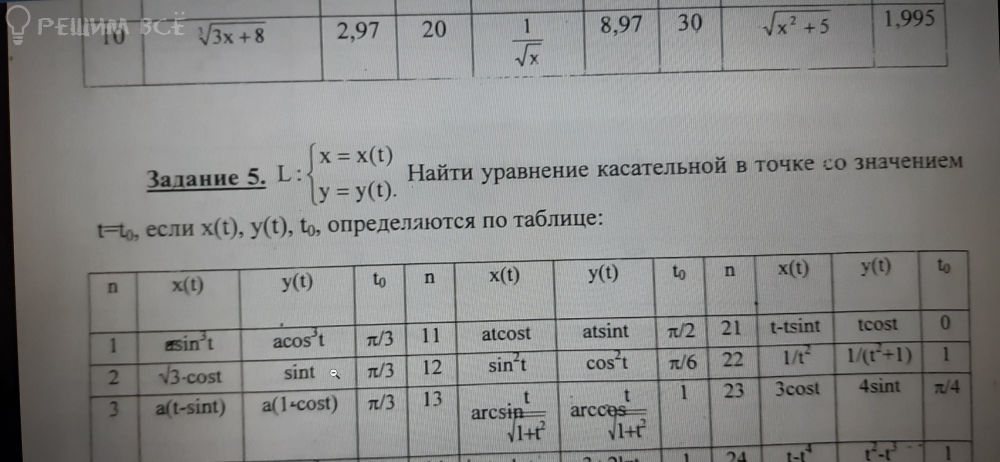
Найти уравнение касательной в точке t=t0.

Значения: x(t)=asin³t,
y(t)=acos³t,
t0=p/3

Составьте уравнение касательной к графику функции y=3–x в точке x=1

Здравствуйте!
Нужно найти абсциссу точки пересечения с осью OX касательно к кривой Y=8 –9/4–x
проходящей через точку (7:8)
Заранее спасибо!

5. Написать уравнение касательной к графику функции y = 0.5(x–1)² в точке с абсциссой x=2

6. Исследовать функцию и построить схематический график

Уравнение касательной
[m]f(x) =4–sinx x0=π/2

Напишите уравнение касательной к графику функции y=3/x в точке x=2

составить уравнение касательной к графику функции y 3x2–2x +8 в точке с абсциссой x0 =1

Напишите уравнение касательной к графику функции y=x²+2x–1 параллельной прямой y=2x+1

запишите уравнение касательной к функции y f(x) при x=x0 1) y=0,2x² – 4 при x0=2. 2)y=–3x²–x при x0=–2. 3)y=x²–1/x при x0=3

В какой точке кривой y²=4x³ касательная к графику ее функции перпендикулярна прямой x+3y–1=0, заранее спасибо

решите все подробно дам 40 баллов

Угловой коэффициент касательной к графику функции f(x)=3x²–7x+3 в точке х=1 равен

Пря­мая y=–3x–6 па­рал­лель­на ка­са­тель­ной к гра­фи­ку функ­ции f(x)=x²+7x–4 . Най­ди­те абс­цис­су точки ка­са­ния.

Найти уравнения касательной и нормали к данной кривой в данной точ–
ке:

7.1.164. y = x³, x0 = –2.

Помогите с 24 и 25, пожалуйста
С идеей хотя бы

Написать уравнение кривой, проходящей через точку (2; –1) и имеющей касательную с угловым коэффициентом равным 1 / 2y

Найди все значения параметров b и c, при которых прямая y=3x−15 касается параболы f(x)=x2+bx+c в точке (5;0).

Записать уравнение нормали к кривой y=3tg2x+1, в точке с абсциссой х=pi/2

043.29. Напишите уравнения касательных к графику функции y = f(x) в точках его пересечения с осью абсцисс, если:

г) f(x) = x³ − x⁴.

Найди, в какой точке графика функции y=f(x) касательная параллельна заданной прямой:

y=7+3x, f(x)=x³/3−3x²+12x−7.

Ответ (при необходимости округли с точностью до десятых):

Найти уравнения касательной и нормали к кривой
4x³ – 3xy² + 6x² – 5xy – 8y² + 9x + 14 = 0 в точке M(–2, 3).

Найдите угловой коэффициент касательной к графику функции:
f(x)=0,5x²–1 в точке Х0=–3

Найдите угол наклона касательной
к графику функции f(x)=1/3x³+5 в точке с абсциссой Х0=–1

Напишите уравнение касательной к графику функции f(x)x²+2x+1 в точке с абсциссой Х0=–2

1. Найдите экстремумы функции у = х3 – 6х2. 2. Найдите промежутки возрастания и убывания функции у = –х2 + 2х – 3 3. Составьте уравнение касательной к графику функции у = х3 – х2 в точке с абсциссой х0 = 1. 4. Найдите наибольшее и наименьшее значение функции у = 4х + х3 на отрезке [0; 3].
хээээээээээлп

Найди, в какой точке графика функции y=f(x) касательная параллельна заданной прямой:

y=1+2x, f(x)=x33−5x2+27x−10.

Напишите уравнение касательной к графику функции H(x)=x²–x–1 в точке с абсциссой x=–2

Найди тангенс угла наклона касательной, проведённой к графику функции f(x) = (x – 7)(x² + 7x + 49) в точке с абсциссой x₀ = 3.

41.44. Определите абсциссы точек, в которых касательная к графику функции y = h(x) образует с положительным направлением оси абсцисс заданный угол α:
a) f(x) = x² – 3x + 19, α = 45°;
б) f(x) = 4/(x + 2), α = 135°.

Найди тангенс угла наклона касательной, проведённой к графику функции f(x)=(x−4)(x²+4x+16) в точке с абсциссой x0=1.

Напиши уравнение касательной к графику функции y=6/x в точке x=2,5.

Найди a, при которых касательная к параболе y=3x²+4x+2 в точке x0=3 является касательной к параболе y=5x²−4x+a.
(Ответ вводи в виде сокращённой дроби:
1) если получается целое число, в знаменателе пиши 1.
2) Минус пиши в числителе)

К графику функции y=x³/3 провести касательную так, чтобы она была параллельна прямой y=4x−4.

Уравнения касательных: