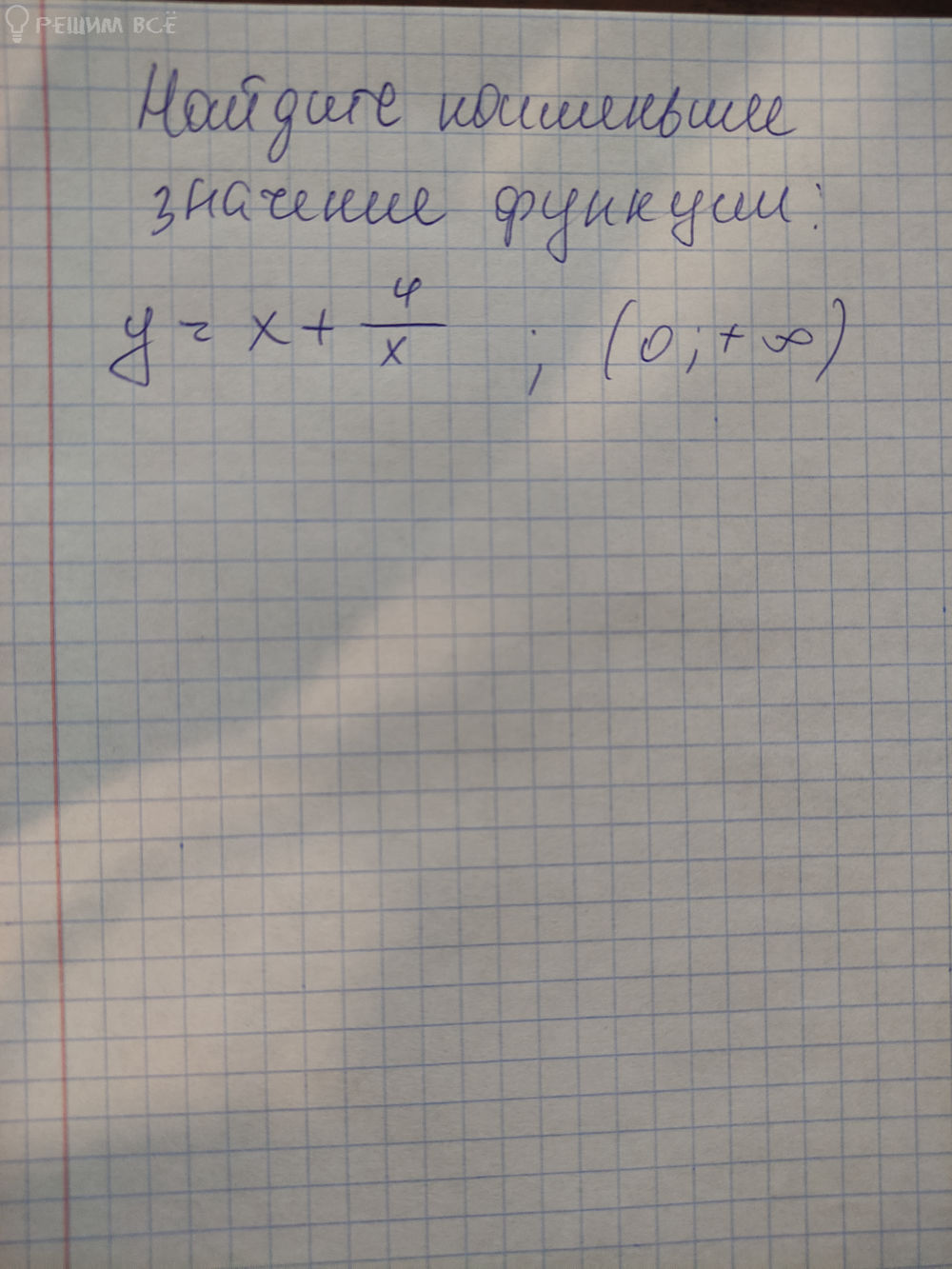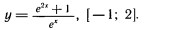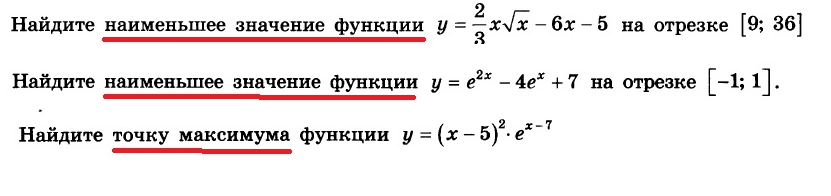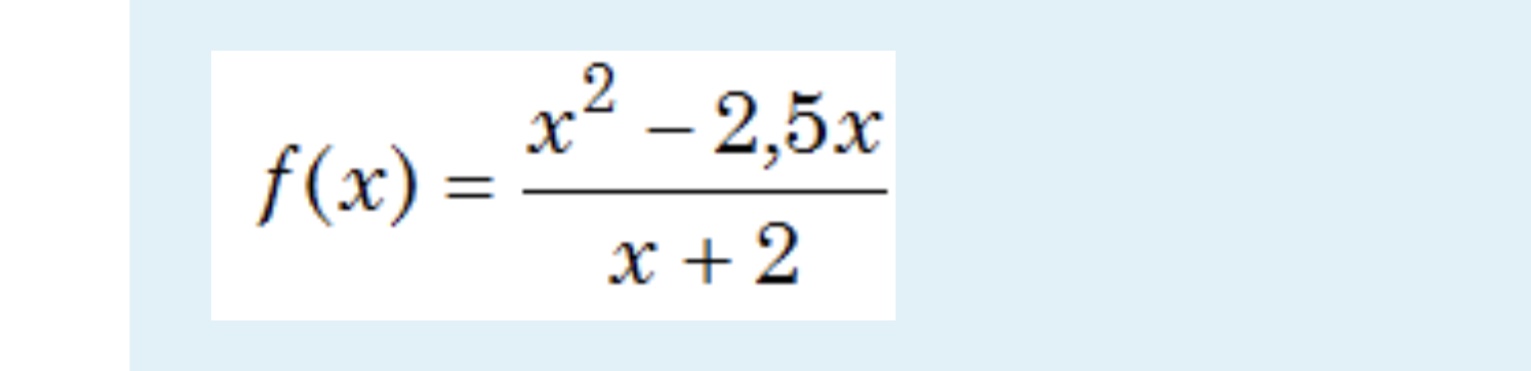Наибольшее наименьшее значение, возрастание,убывание

12 номер ЕГЭ проф. мат????
Найдите наименьшее значение функции у=–6ln(x+5) +6x–1 на отрезке [–4, 5;0]

y = e^2x2+1 × ( x² – 3/2 ) исследовать на монотонность и экстремумы

Буду очень признателен, если будет решение до 7:00 по мск

Заранее Всем спасибо, за Ваш труд

5 Найти промежутки монотонности функции:

f(x) = – 1/4 x⁴ – x + 1

6 Исследовать на экстремум и точки перегиба кривую:

f(x) = x³ + 6x² + 9x + 8

Докажите ,что в области определения является убывающей функция:
1)f(x)=–2x+8
2)f(x)=10/x

необходимо покрыть плиткой пол и стены бассейна, затратив 216 квадратных метров плитки. бассейн должен иметь форму прямоугольного параллелепипеда с открытым верхом, длина которого в два раза больше ширины. найдите длину, ширину и высоту бассейна, обьем которого является наибольшим .

Очень нужноГа ! T e L 1 п'. На т Hougqure e = е ”;‘–Е'. | : : !` _‚ [’,’. T – ‚ et Ll е _‚'", ! | ) ’t, т ы . ННЕа _. г_…і“––—х e В ННННЕБ e o e 1] "l––l'lIlI" £ e – ll.“l l==––= 1 ..=–I..===. ННЕ ЕВГа .l========== P o .=I––==Il–=='ll= —Н Y ey | P bl B | –_С–.ь__і · Н ' = –==..–==–.– –– ЕЫНа | .......'.... г — L T Ll !ll="lll–"' – . Е ЕЕЕг ' '”gg%==i=====i==== ее 1 =N НЕ _@Ё;‚;Ёёг... Нн, e v —_–Ъ‹ё@@ЁЁ‚!–'.=.'!Ц. g НОНЕ НЫ L Sk ok I MBEmaE –

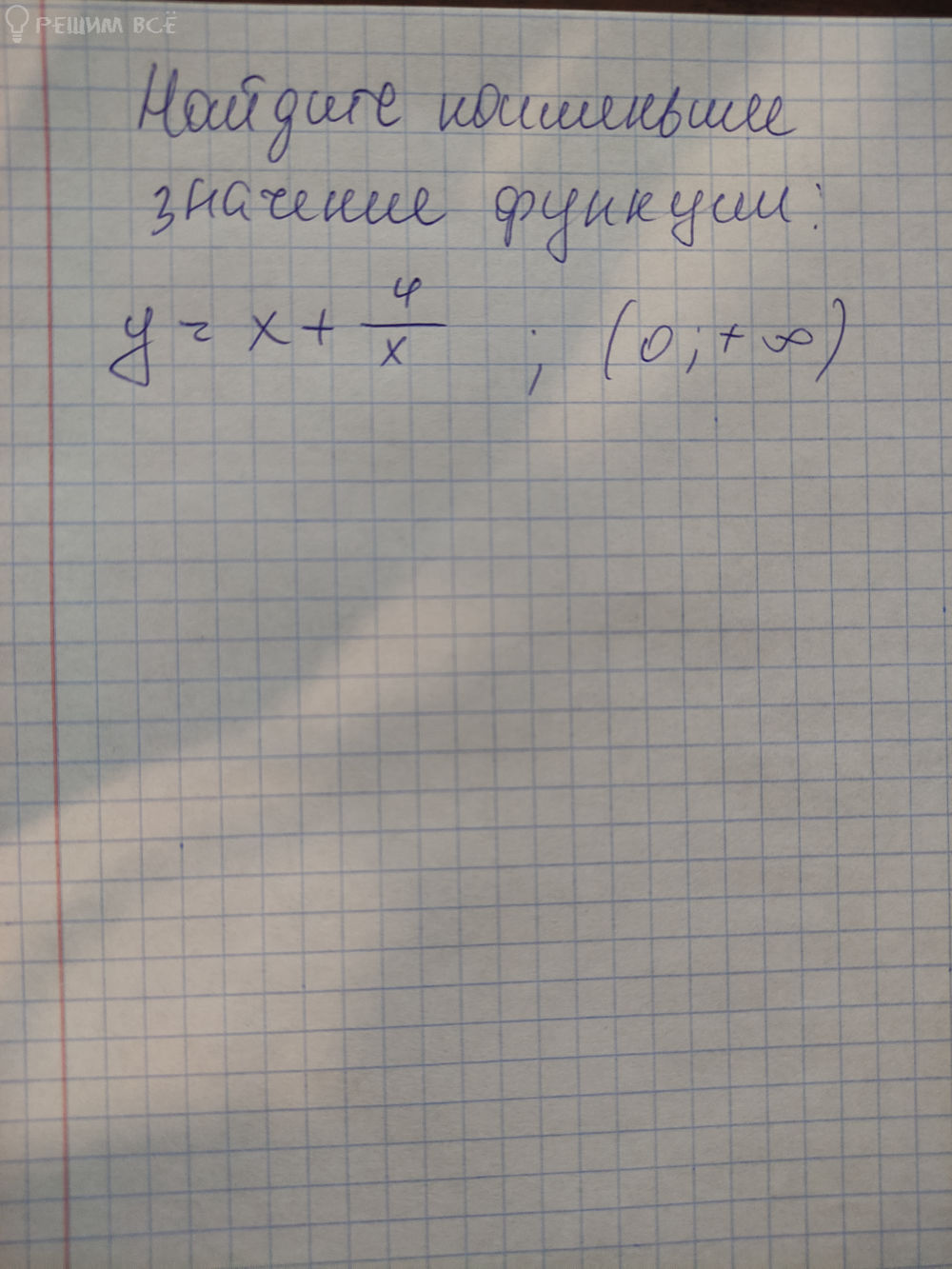
Найдите наибольшее и наименьшее значение функции на отрезке.

x⁵ + 15x³ – 50x, [–4; 0]

Локальный минимум функции f(x)=x(x²−9)

Найдите промежутки монотонности функции У=х⁴−4х²+4

Провести полное исследование функции с помощью первой и второй производной, построить ее график. Найти наибольшее и наименьшее значения на указанном отрезке.

Очень прошу о помощи!!! решить три задания. 1–2) составить уравнение касательной к графику функции в точке х0. 3 )исследовать функцию на монотонность и экстремумы.
очень–очень нужны правильные ответы. напрямую зависит годовая оценка????

Найти точку максимума Функции y=2x–lnx

Задание 3–7

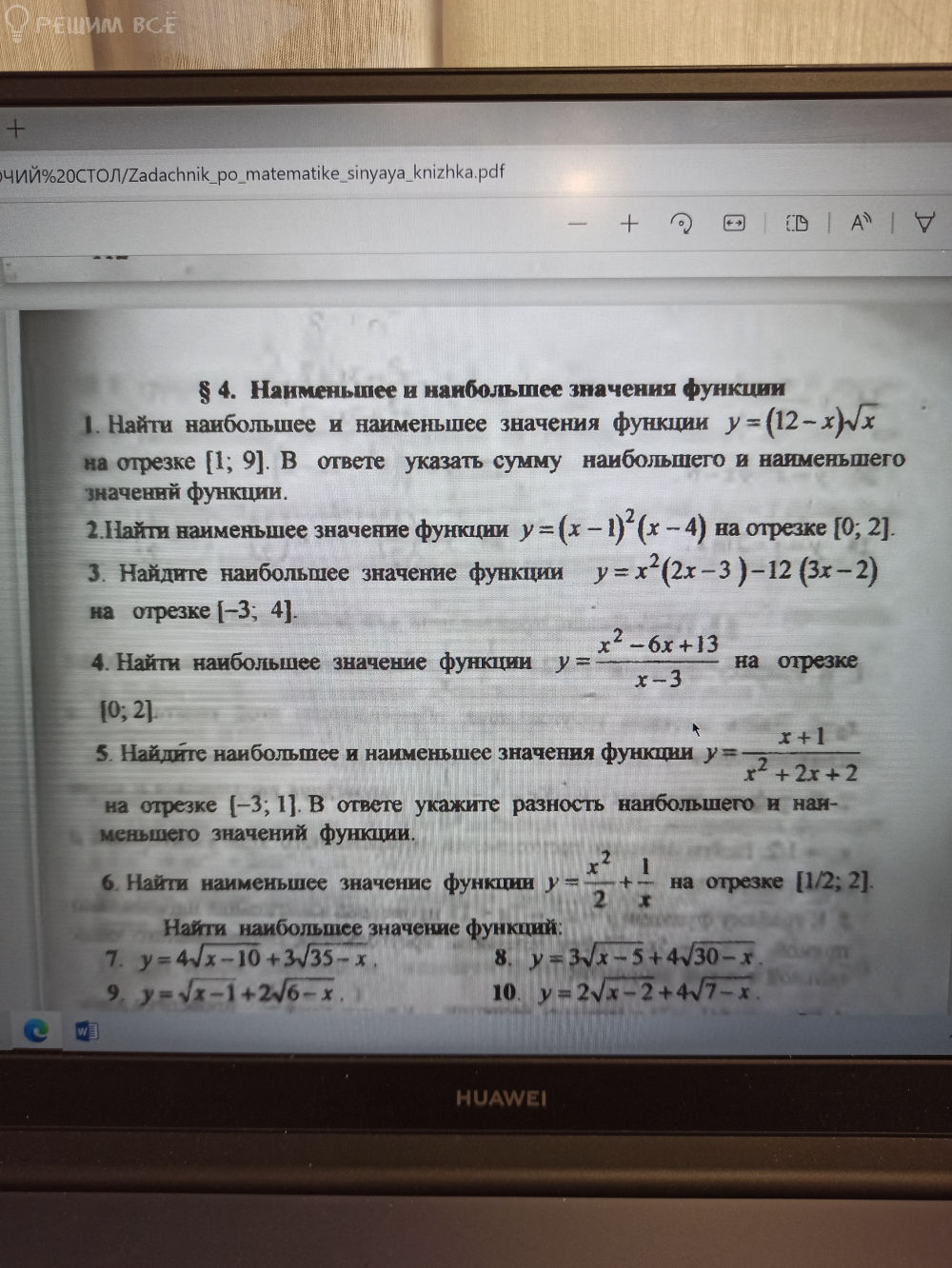
Найти наименьшее и наибольшее значения функции y=f(x)
на заданном отрезке [a;b]:

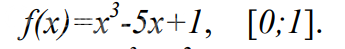
Найти наибольшее и наименьшее значение функции на отрезке

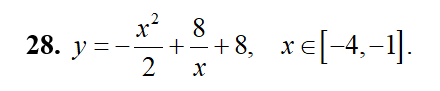
Найдите точку максимума: y=lnx–2x
Найлити точку минимума:
y=(x–7)e^x+7

Найти наибольшее и наименьшее значения функции на указанном множестве
1.????=2√????−????, [0;4] 2.????=2√????−1−????+2, [1;5]
3.????=− 10????+10 , [−1;2] ????2+2????+2
4.????=10????, [0;3] 1+????2
5.????=3−????− 4 [−1;2] (????+2)2
6.????=????−4√????+2+8, [−1;7] 7.????=8????+ 4 −15, [0,5;2]
8.????= 4???? , [−4;2] 4+????2
9.????=????−4√????+5, [1;9]
10.????=4−????− 4, [1;4]

17. Функция у = f (х) задана на oTpe3ke [g; b]. YKakuTe KOTHYECTBO TOYEK MAKCHMYMa функции, если график её производной имеет вид

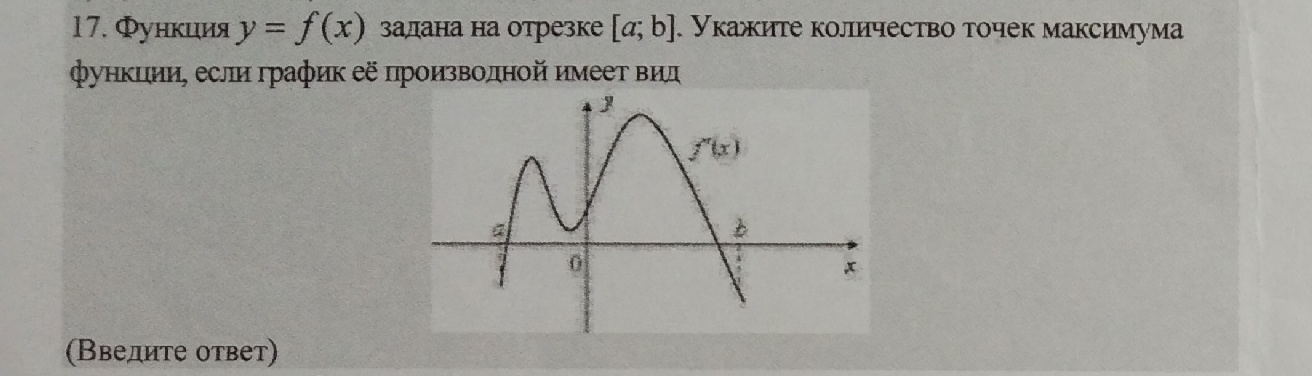
18. Функция у = f(х) задана на отрезке [а; b]. Укажите количество точек минимума функции, если график её производной имеет вид... _ :

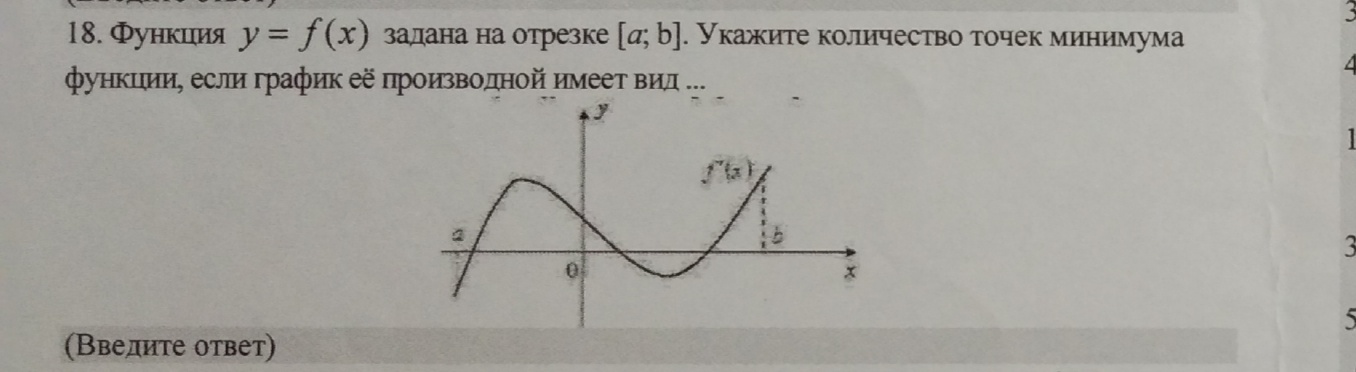
Найдите промежутки возрастания функции f(x)=x3–x2–x+8

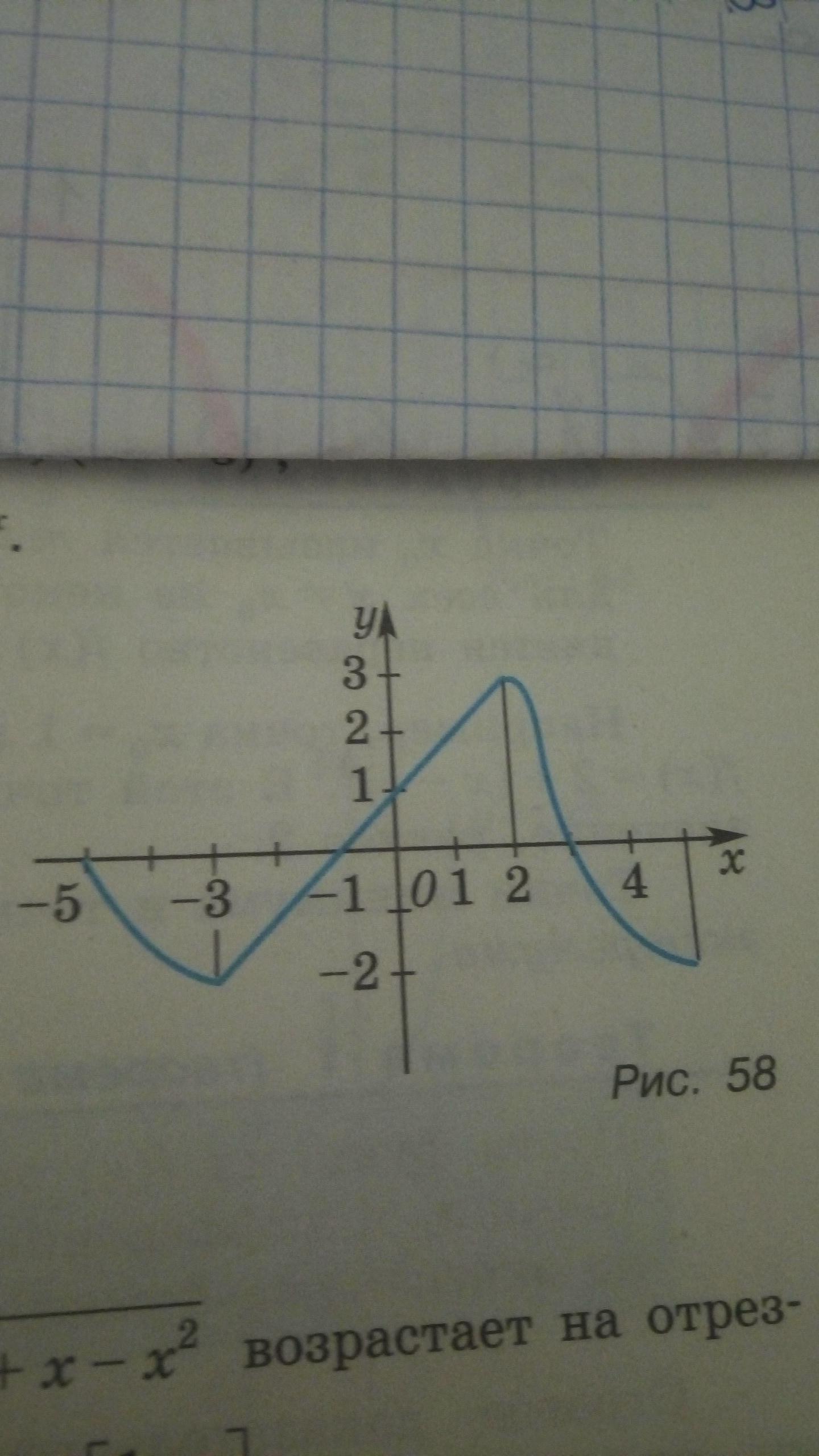
На рисунке 58 изображен график функции f'(x), является производной функции y. Определить промежутки возрастания и убывания функции y=f(x).

Точка экстремума функции y'(x) непрерывной на всей числовой оси, если y'=(x+1)²(x–2)

☐ x=2 – точка максимума

☐ x=2 – точка минимума

☐ x=–1 – точка максимума

☐ x=–1 – точка минимума

☐ точек экстремума нет

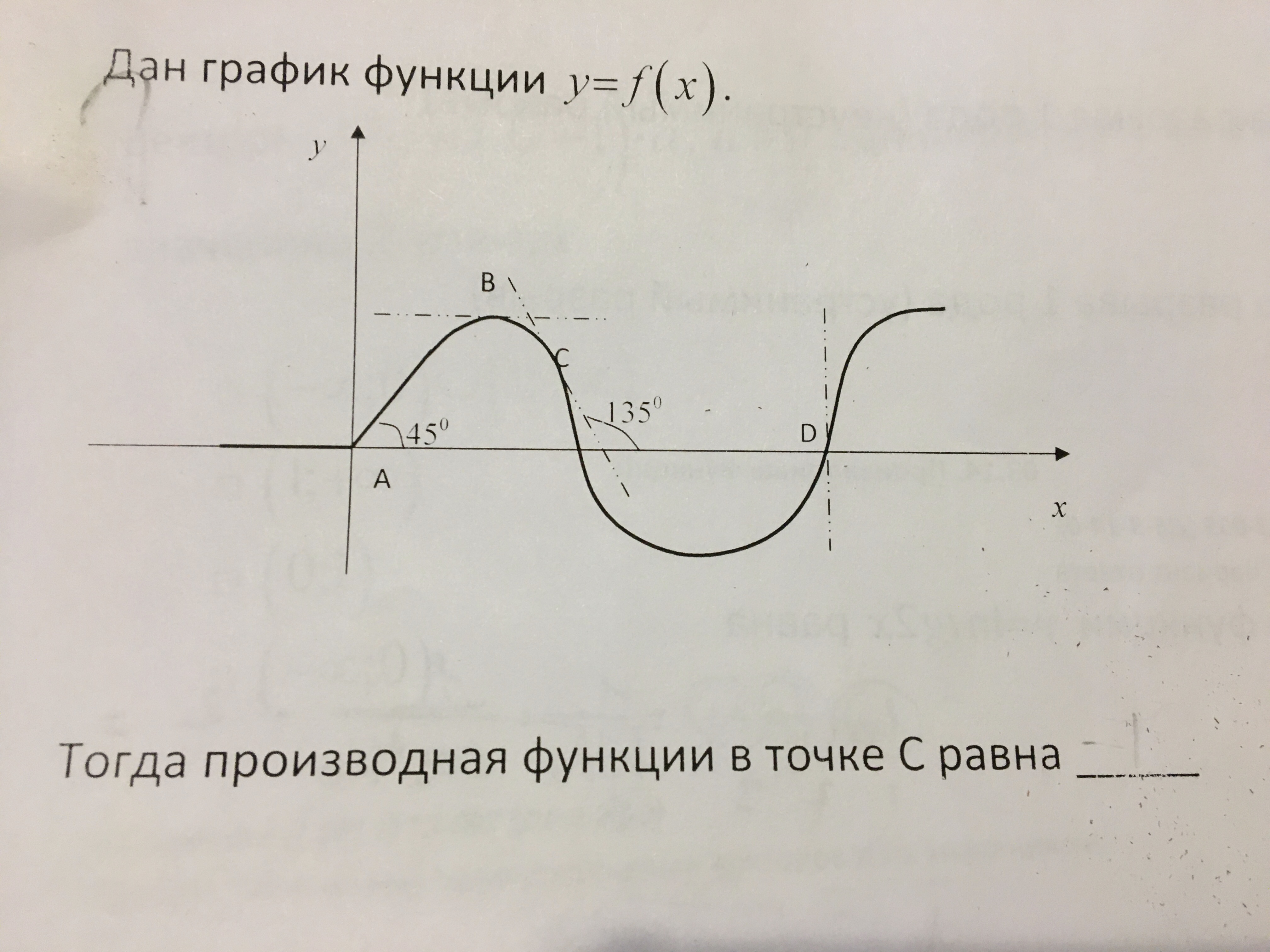
Дан график функции y = f(x).


Тогда производная функции в точке C равна ___

Найти наибольшее значение функции y = x³ + (–6) · x² + (9) · x + (–4) на отрезке 1 ≤ x ≤ 5.

y=13x–10sin x–1 наименьшее значение на отрезке [0;π/2]

Найдите наименьшее и наибольшее значение функции на промежутке: 1) y = x³ – 6x² + 9 на отрезке [–1, 2], 2) y = x⁴ – 8x² + 3 на отрезке [–3, 3].

Исследуйте на монотонность и экстремумы функцию:

f(x) = x²/12 – 6lnx.

Исследуйте функцию на экстремум / f(x)=4x³–12x³–3

Найдите наибольшее значение функции [m]y=\frac{\pi }{2}sinx-\sqrt{5}x+1[/m] на отрезке [m][0;\frac{\pi }{4}][/m]

Найдите наибольшее значение функции y = √35 + 2x – x².

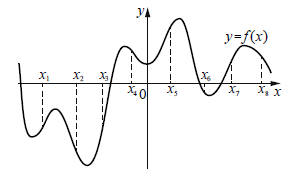
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, ..., x8.


Найди все отмеченные точки, в которых производная функции y=f(x) положительна. В ответ укажи количество этих точек.

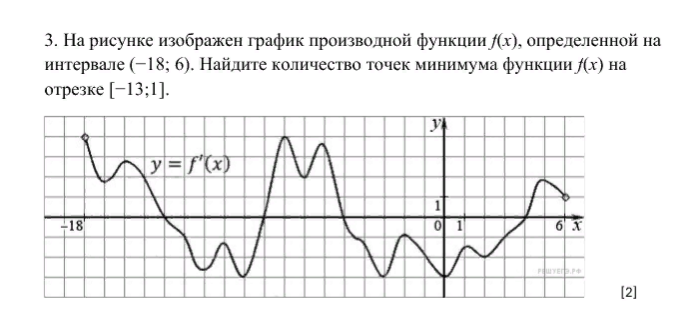
3. На рисунке изображен график производной функции f(x), определенной на интервале (–18; 6). Найдите количество точек минимума функции f(x) на отрезке [–13; 1].

найдите наименьшее значение функции f(x)=x⁴–2x²+5 на отрезке [–2;0.5]

пожалуйста подробно

3)найти наименьшее и наибольшее значения функции y=f(x) на отрезке [a; b] (скрин прикрепил)
y=e2x +1/ex, [–1;2]

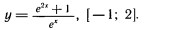
Найдите наименьшее значение функции
y=(2x–14)×e^x–6
На отрезке [5;7]

НАЙДИТЕ ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ f(x) = xвкуб–3xв кадрат –4

ПОМОГИТЕ РЕШИТЬ ДАЮ 100 БАЛЛОВ

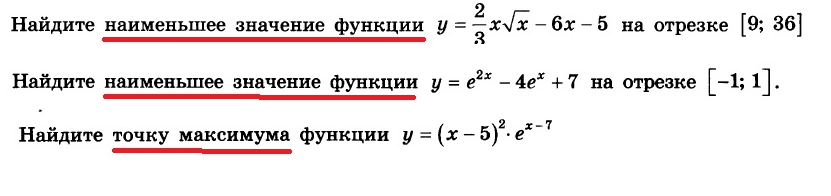
Помогите решить пожалуйста 3.1 и 3.2

Найти промежутки возрастания и убывания и экстремумы функции

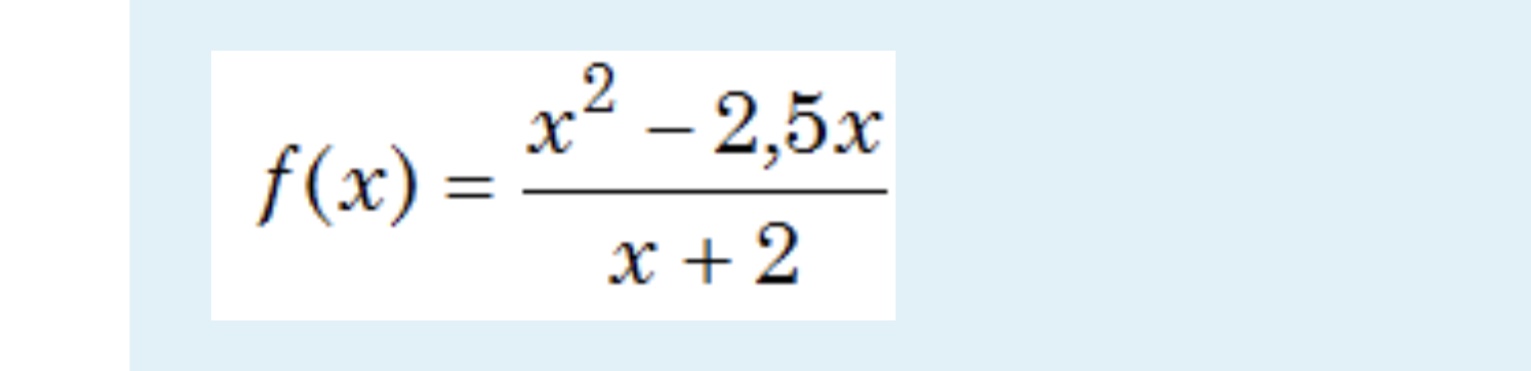
1. Найдите экстремумы функции у = х3 – 6х2. 2. Найдите промежутки возрастания и убывания функции у = –х2 + 2х – 3 3. Составьте уравнение касательной к графику функции у = х3 – х2 в точке с абсциссой х0 = 1. 4. Найдите наибольшее и наименьшее значение функции у = 4х + х3 на отрезке [0; 3].
хээээээээээлп

Найдите точку минимума функции y = – x / (x² + 324)

Найдите наибольшее значение функции y = 85x – 83 sin x + 55 на отрезке [–π/2; 0]

Докажите ,что в области определения является возрастающей функция:
1)f(x)=14+5x
2)f(x)=– 3/x

ПОЖАЛУЙСТА ПОМОГИТЕ СДЕЛАТЬ ВСЕ 4 ПРИМЕРА ,ЗАДАНИЕ ПО НОВОЙ ТЕМЕ (НЕ ПРОХОДИЛИ)
Найдите промежутки возрастания и убывания функции y=f(x)
1)f(x)=7x+1
2)f(x)=–2x–13
3)f(x)=x²–3x
4)f(x)=8–x³

Найдите промежутки возрастания и убывания функции y=f(x)
f(x)=–x²–8x+9

Найдите экстремумы функции y=f(x)
f(x)=2/x +x²(+х² это уже отдельно от дроби )