Задача 56567 Найти наибольшее значение функции...
Условие
математика ВУЗ
401
Решение
★
y`=0
3x^2-12x+9=0
x^2-4x+3=0
x_(1)=1; x_(2)=3
[1] ___-__ (3) __+____ [5]
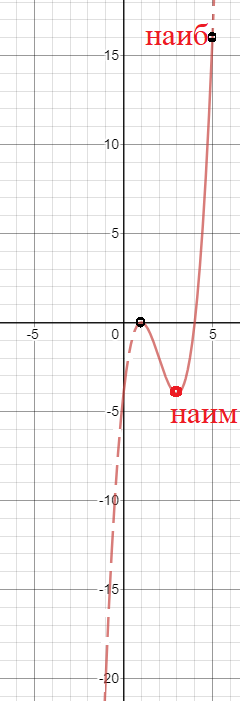
x=3 - точка минимума, в ней не может быть наибольшего значения
Находим значения на концах отрезка
y(1)=1^3-6*1^2+9*1-4=0
y(5)=5^3-6*5^2+9*5-4=16 - [b] наибольшее[/b]
