ПРОИЗВОДНАЯ и ее применение
О категории
Нахождение производных по формулам и правилам. Уравнение касательной и нормали. Наибольшее, наименьшее значение
Подкатегории (3)
Вычисление производной по правилам и формулам 73
Наибольшее наименьшее значение, возрастание,убывание 46
Уравнение касательной, уравнение нормали, угловой коэффициент касательной 46
Практика (47)
f(x)=1/x,[1/3;1/2]
f(x) = |x-1|; [0; 3]
а) f(x)=x^4-4x^2
б) f(x) = ((x+1)/(x+2))^2
sin 44◦
1) Вычислить производную функции:
2) Вычислить частные производные функций нескольких переменных:
3) Найти экстремальные точки функции:
у = (x-1)(x-2)
Определить наличие максимума (минимума) в этих точках.


0,93^(5)
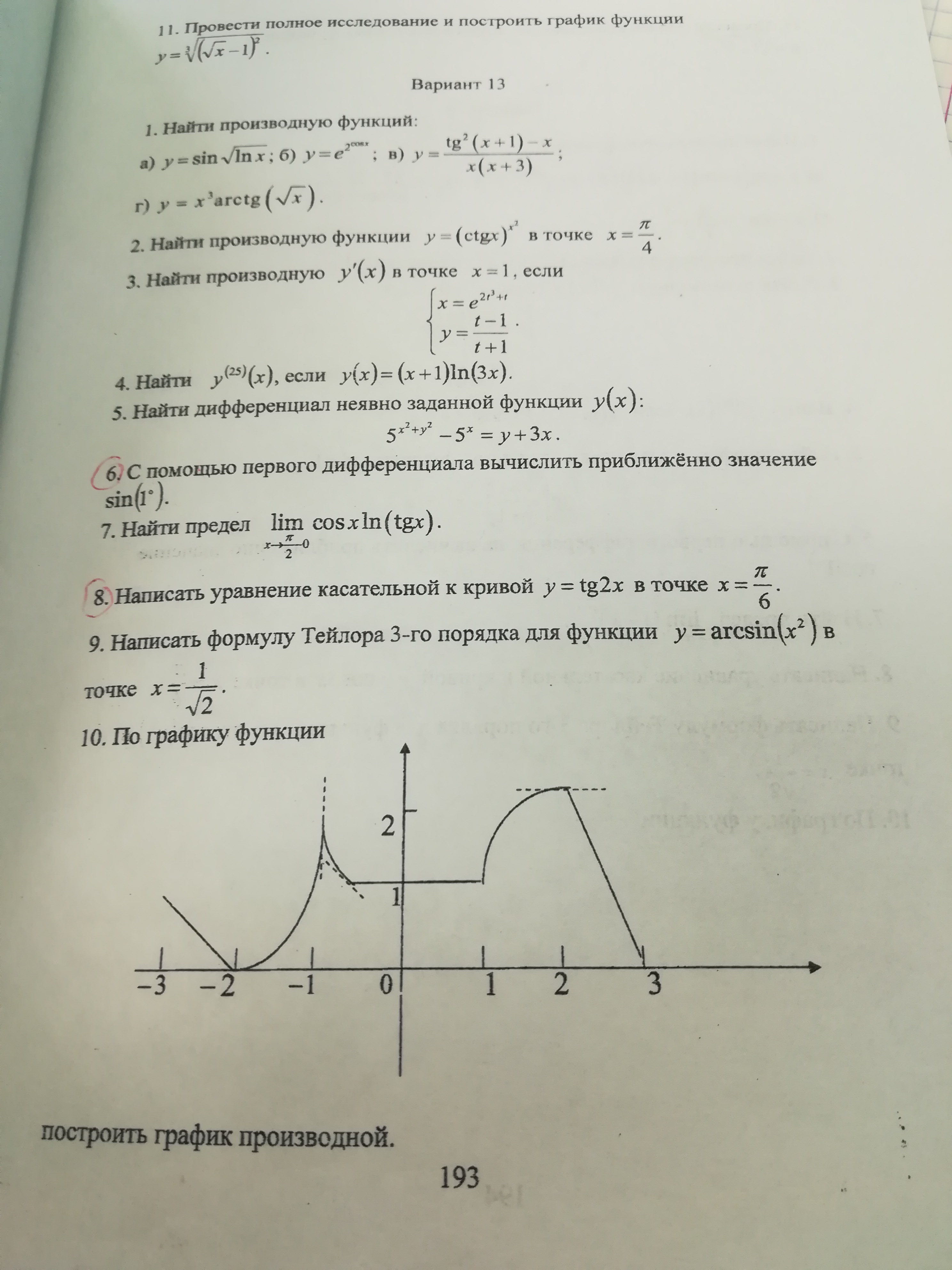

y=2^(cos x)


cos^2(x + y) = x * y
составить уравнения касательной и нормали к кривой, найти min max значение функции, исследовать функции
срочно!
f(x) = √(2 - x), x_0 = -7.
а) Y= x/√(4-x); б)y=ln〖(1+〗 x^2)
y' - ?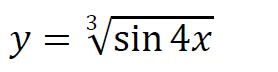
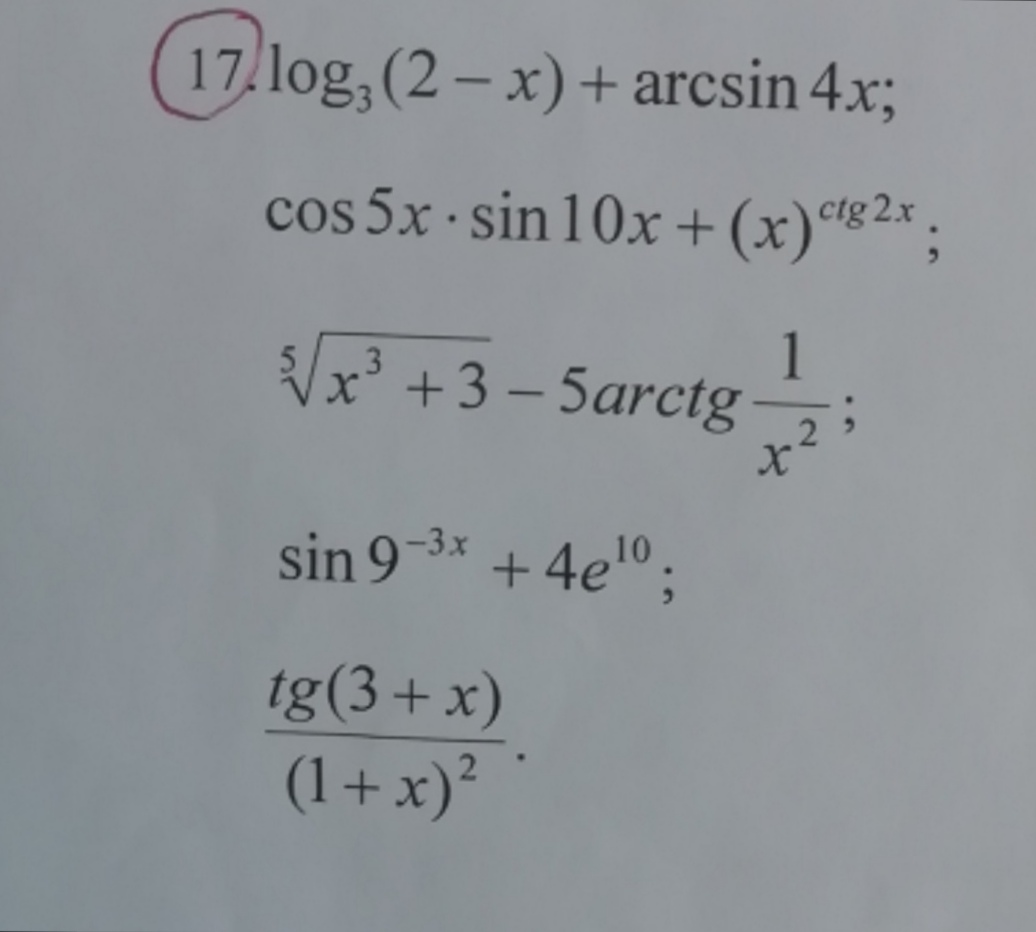
1) 7cos5x-2^(x+3)
2) sin4x*e^(3x)+(cos4x)^x
...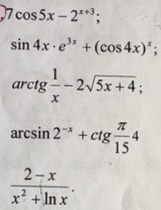
y=(sinx)^(x^2)
y = x² + ln(x² + 1) tg³(5 cos x - 7)
y' =
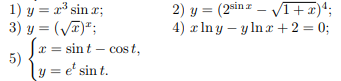
Пожалуйста, очень нужен развёрнутый ответ, препод требует детально расписывать каждый шаг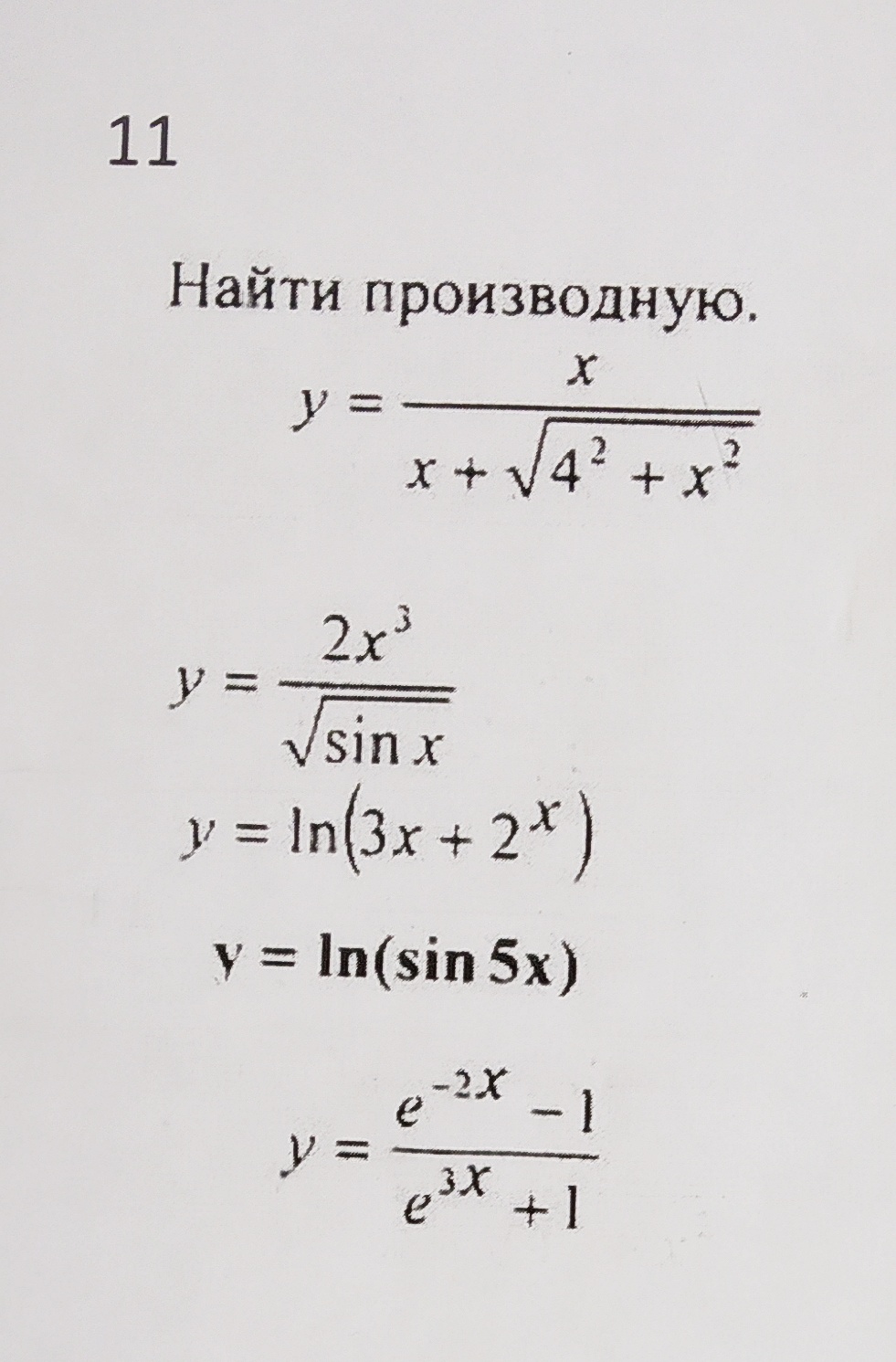
вычисления производных.
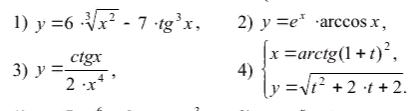
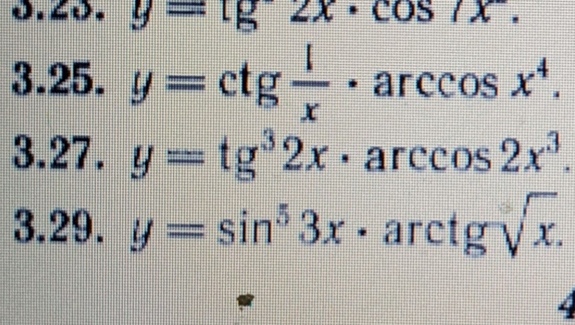
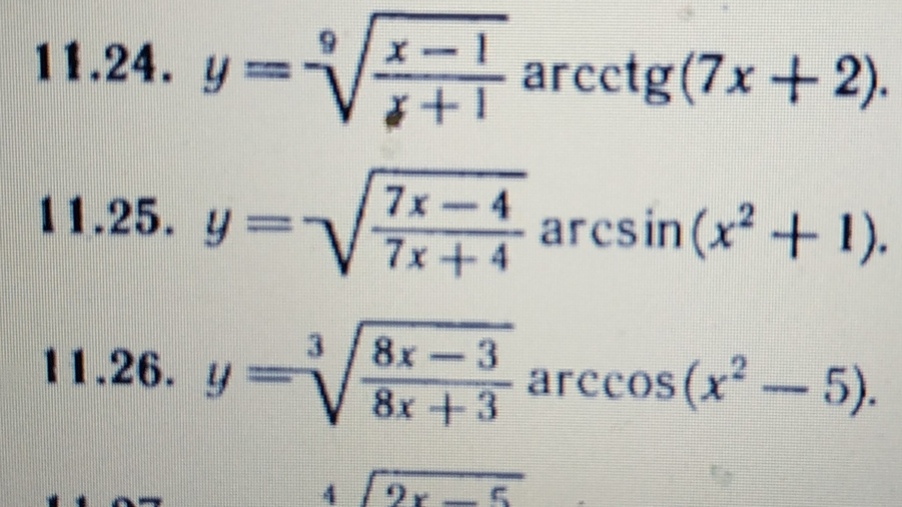
Редакторы (1)
 SOVA
SOVA
Создатель


