Задача 33740 найти производную от функции 1)...
Условие
1) 7cos5x-2^(x+3)
2) sin4x*e^(3x)+(cos4x)^x
...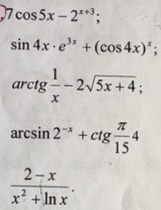
Решение
1.
y`=7*(cos5x)`-(2^(x+3))`
y`=7*(-sin5x)*(5x)`- 2^(x+3)*(x+3)`*ln2
y`=-35sin6x -ln2*(2^(x+3)
2.
y`=(sin4x)`*(e^(3x))+(sin4x)*(e^(3x))`+(cos4x)^(x)*((x)`*lncos4x+(x)/(cos4x)) *(cos4x)`)
вычисление производной второго слагаемого по формуле
производная показательно-степенной функции
(см. приложение)
y`=(cos4x)*(4x)`*(e^(3x)+(sin4x)*(e^(3x))*(3x)`+
+(cos4x)^(x)*(lncos4x+(-4xsin4x)/(x)) )
3.
y`=(arctg(1/x))`-2*(sqrt(5x+4))`=
=(1/(1+(1/x^2)^2)) * (1/x^2)`- 2*(1/(2*sqrt(5x+4)))*(5x+4)`=
=(1/(1+(1/x^2)^2)) * (x^(-2))` -(5/sqrt(5x+4))
=(-2x/(x^2+1)) - (5/sqrt(5x+4))
4.
y`=(arcsin2^(-x))`+(ctg(π/15)*4)`=(1/sqrt(1-(2^(-x))^2))*(2^(-x))` + 0=
=(1/sqrt(1-2^(-2x))*(2^(-x))*(ln2)*(-x)`=
= - ln2*(2^(-x)/sqrt(1-2^(-2x))
5.
y`=[b]([/b]((2-x)`*(x^2+lnx) - (2-x)*(x^2+lnx)`[b])[/b]/(x^2+lnx)^2
y`=[b]([/b]-1*(x^2+lnx)-(2-x)*(2x+(1/x)) [b])[/b]/(x^2+lnx)^2
