Задача 46291 Найти промежутки возрастания и убывания...
Условие
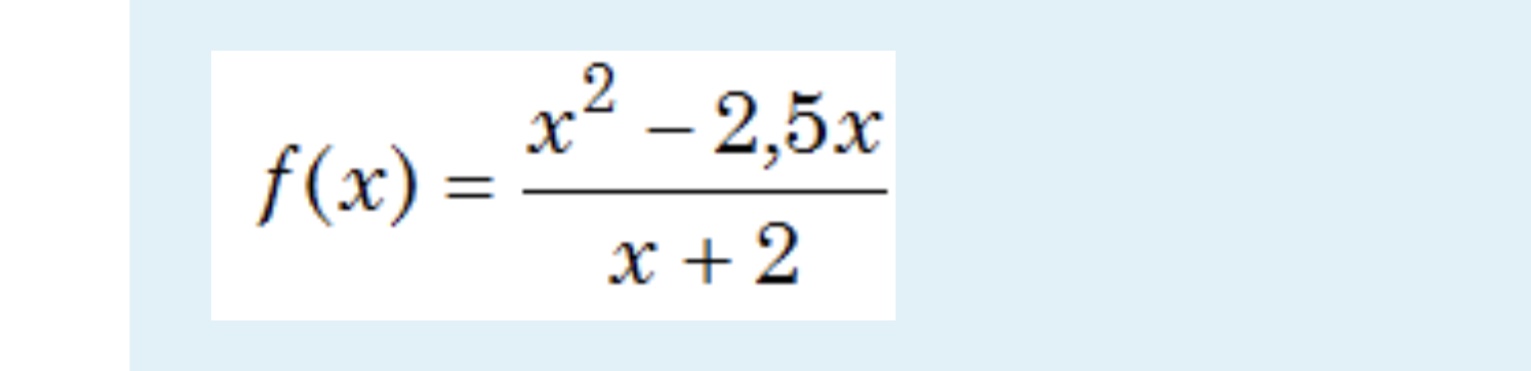
математика 10-11 класс
905
Все решения
х+2 ≠ 0 ⇒ х ≠ -2
Находим производную по правилу производная частного:
f `(x)=((2x-2,5)*(x+2)-(x^2-2,5x))/(x+2)^2
f `(x)=(2x^2-2,5*x+4x-5-x^2+2,5x)/(x+2)^2
f `(x)=(x^2+4x-2,5)/(x+2)^2
f ` (x)=0
x^2+4*x-5=0
х+2 ≠ 0 ⇒ х ≠ -2 не входит в область определения
D=16+20=36
x_(1)=(-4-6)/2; x_(2)=(-4+6)/2
x_(1)=-5; x_(2)=1
Расставляем знак производной:
_+__ (-5) __-__(-2) __-___ (1) _____+___
x=-5 - точка[b] максимума[/b], производная меняет знак с + на -
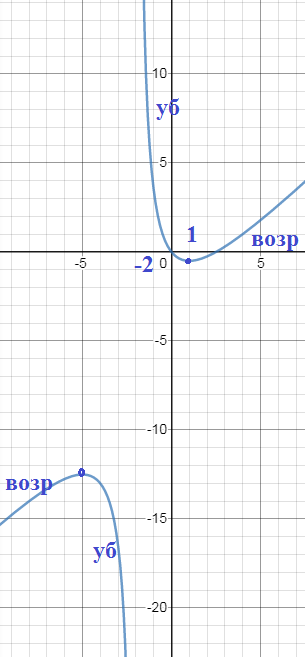
См. рис.
x=1- точка [b]минимума[/b]
Возрастает
x ∈ (- ∞; -5) и (1;+ ∞ )
Убывает
x ∈ (-5;-2) и (-2;1)