Задача 52975 Исследуйте функцию на экстремум /...

vk284147118

2020-08-06 14:47:08

Исследуйте функцию на экстремум / f(x)=4x^3-12x^3-3

sova

2020-08-06 15:13:37

ОПЕЧАТКА в условии:
f (x)=4x^3-12x^([b]2[/b])-3

f `(x)=(4x^3-12x^2-3)`

Применяем правила вычисления производных:
производная суммы равна сумме производных

f `(x)=(4x^3)`+(-12x^2)`+(-3)`

постоянный множитель можно выносить за знак производной:

f`(x)=4(x^3)`-12(x^2)`-(3)`

По таблице:
(x^3)`=3x^2
(x^2)`=2x
(C)`=0 ⇒ (3)`=0


y`=4*3x^3-12*2x

y`=12x^2-24x

y`=12x*(x-2)

y`=0

12x*(x-2)=0

x=0 или x-2=0 ⇒ x=2

Это точки, в [i]которых производная равна 0. [/i]
Чтобы узнать есть в них экстремум или нет надо применить
теорему ( достаточное условие существования экстремума ):
если в точке х_(о) производная равна 0
и
[i]при переходе через точку [/i] х_(о) производная меняет знак + на -,
то х_(о) - [i]точка максимума[/i]
( если же производная меняет знак - на +, то х_(о) - [i]точка минимума[/i])

В других случаях (при смене знака + на + или - на - ) [b]экстремума нет
[/b]

Находим знак производной.

y`=12x^2-24x

Производная - то же [i]функция.[/i]

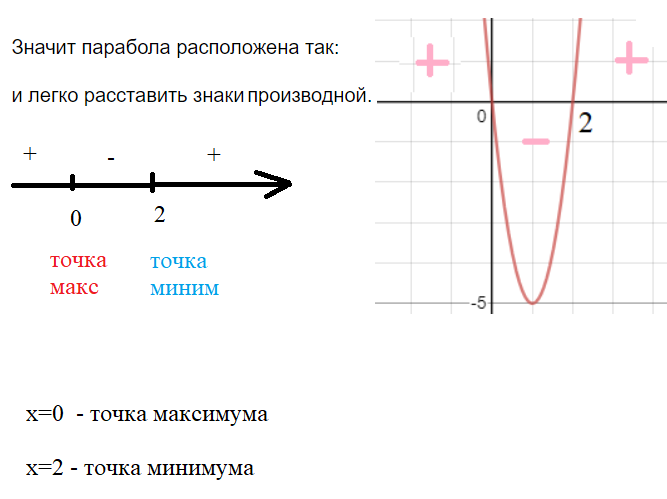
В данном случае это [i]квадратичная функция[/i], графиком служит парабола, ветви вверх

Нашли нули этой функции: x=0; x=2